Question

求由曲線y=x²與y=2-x²所圍成圖形的面積為    ．

Answer 1

【答案】分析：作出兩個曲線的圖象并求出它們的交點坐標．利用定積分公式并結合函數圖象的對稱性，可得所求面積為函數  2-2x²在區間[0，1]上的定積分值的2倍，再加以運算即可得到本題答案．
解答：解：∵曲線y=x²和曲線y=2-x²所的交點為（1，1）和（-1，1）
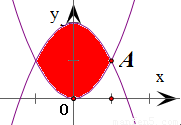
∴曲線y=x²和曲線y=2-x²所圍圖形的面積為
S=2=2
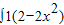
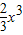
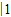
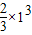
=2（2x-）=2[（2×1-）-（2×0-）]=
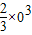
故答案為：
點評：本題求兩條曲線圍成的曲邊圖形的面積，著重考查了定積分的幾何意義和積分計算公式等知識，屬于基礎題．