
【題目】如圖,在正四棱柱ABCD﹣A1B1C1D1中,AB=1,AA1=t,建立如圖所示的空間直角坐標系O—xyz.
(1)若t=1,求異面直線AC1與A1B所成角的大小;
(2)若t=5,求直線AC1與平面A1BD所成角的正弦值;
(3)若二面角A1—BD—C的大小為120°,求實數t的值.

【答案】(1) ![]() .
.
(2) ![]() .
.
(3) ![]() .
.
【解析】分析:(1)先根據坐標表示向量![]() ,
,![]() ,再利用向量數量積求向量夾角,即得異面直線
,再利用向量數量積求向量夾角,即得異面直線![]() 與
與![]() 所成角,(2)先利用方程組解得平面
所成角,(2)先利用方程組解得平面![]() 的一個法向量,利用向量數量積得向量夾角余弦值,再根據線面角與向量夾角互余關系得結果,(3)先利用方程組解得平面
的一個法向量,利用向量數量積得向量夾角余弦值,再根據線面角與向量夾角互余關系得結果,(3)先利用方程組解得平面![]() 以及平面
以及平面![]() 的一個法向量,利用向量數量積得法向量夾角余弦值,再根據二面角與向量夾角相等或互補關系得結果.
的一個法向量,利用向量數量積得法向量夾角余弦值,再根據二面角與向量夾角相等或互補關系得結果.
詳解:(1)當![]() 時,
時,![]() ,,
,,![]() ,
,![]() ,
,![]() ,
,
則![]() ,
,
![]() ,
,
故 ,
,
所以異面直線![]() 與
與![]() 所成角為
所成角為![]() .
.
(2)當![]() 時,
時,![]() ,
,![]() ,
,![]() ,
,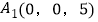 ,
,![]() ,
,
則![]() ,
,![]() ,
,
設平面![]() 的法向量
的法向量![]() ,
,
則由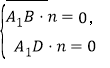 得,
得,![]()
不妨取![]() ,則
,則![]() , 此時
, 此時![]() ,
,
設![]() 與平面
與平面![]() 所成角為
所成角為![]() ,因為
,因為![]() ,
,
則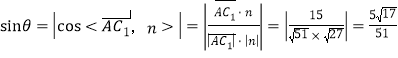 ,
,
所以![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() .
.
(3)由![]() 得,
得,![]() ,
,![]() ,
,
設平面![]() 的法向量
的法向量![]() ,
,
則由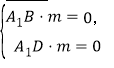 得,
得,![]()
不妨取![]() ,則
,則![]() , 此時
, 此時![]() ,
,
又平面![]() 的法向量
的法向量![]() ,
,
故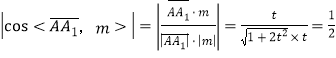 ,解得
,解得![]() ,
,
由圖形得二面角![]() 大于
大于![]() ,所以符合題意.
,所以符合題意.
所以二面角![]() 的大小為
的大小為![]() ,
,![]() 的值為
的值為![]() .
.


 教育世家狀元卷系列答案
教育世家狀元卷系列答案 黃岡課堂作業本系列答案
黃岡課堂作業本系列答案 單元加期末復習先鋒大考卷系列答案
單元加期末復習先鋒大考卷系列答案科目:高中數學 來源: 題型:
【題目】甲乙兩名籃球運動員分別在各自不同的5場比賽所得籃板球數的莖葉圖如圖所示,已知兩名運動員在各自5場比賽所得平均籃板球數均為10.

(1)求x,y的值;
(2)求甲乙所得籃板球數的方差![]() 和
和![]() ,并指出哪位運動員籃板球水平更穩定;
,并指出哪位運動員籃板球水平更穩定;
(3)教練員要對甲乙兩名運動員籃板球的整體水平進行評估.現在甲乙各自的5場比賽中各選一場進行評估,則兩名運動員所得籃板球之和小于18的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點P為函數f(x)=lnx的圖象上任意一點,點Q為圓[x﹣(e+ ![]() )]2+y2=1任意一點,則線段PQ的長度的最小值為( )
)]2+y2=1任意一點,則線段PQ的長度的最小值為( )
A.![]()
B.![]()
C.![]()
D.e+ ![]() ﹣1
﹣1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐E﹣ABCD中,平面EAD⊥平面ABCD,DC∥AB,BC⊥CD,EA⊥ED,且AB=4,BC=CD=EA=ED=2. 
(1)求證:BD⊥平面ADE;
(2)求直線BE和平面CDE所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知關于x的不等式:|2x﹣m|≤1的整數解有且僅有一個值為2.
(Ⅰ)求整數m的值;
(Ⅱ)已知a,b,c∈R,若4a4+4b4+4c4=m,求a2+b2+c2的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在底面為正方形的四棱錐S﹣ABCD中,SA=SB=SC=SD,異面直線AD與SC所成的角為60°,AB=2.則四棱錐S﹣ABCD的外接球的表面積為( ) 
A.6π
B.8π
C.12π
D.16π
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設某大學的女生體重y(單位:kg)與身高x(單位:cm)具有線性相關關系,根據一組樣本數據(xi,yi)(i=1,2,…,n),用最小二乘法建立的回歸方程為![]() =0.85x-85.71,則下列結論中不正確的是
=0.85x-85.71,則下列結論中不正確的是
A. y與x具有正的線性相關關系
B. 回歸直線過樣本點的中心(![]() ,
,![]() )
)
C. 若該大學某女生身高增加1cm,則其體重約增加0.85kg
D. 若該大學某女生身高為170cm,則可斷定其體重比為58.79kg
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)=lnx+ ![]() +ax(a∈R),g(x)=ex+
+ax(a∈R),g(x)=ex+ ![]() .
.
(1)討論f(x)的極值點的個數;
(2)若對于x>0,總有f(x)≤g(x).(i)求實數a的取值范圍;(ii)求證:對于x>0,不等式ex+x2﹣(e+1)x+ ![]() >2成立.
>2成立.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com