
【題目】已知函數![]() .
.
(Ⅰ)若![]() ,試討論函數
,試討論函數![]() 的單調性;
的單調性;
(Ⅱ)設![]() ,當
,當![]() 對任意的
對任意的![]() 恒成立時,求函數
恒成立時,求函數![]() 的最大值的取值范圍.
的最大值的取值范圍.
【答案】(I)詳見解析;(II)![]() .
.
【解析】試題分析:(Ⅰ)求導得![]() .結合
.結合![]() ,可得
,可得![]() 在
在![]() 上遞減,在
上遞減,在![]() 上遞增.
上遞增.
(Ⅱ)由![]() 對任意的
對任意的![]() 恒成立 可得
恒成立 可得![]() .又由(Ⅰ)知,當
.又由(Ⅰ)知,當![]() 時,
時, 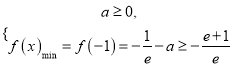 ,可得
,可得![]()
對![]() 求導,研究其最值,并求其范圍即可
求導,研究其最值,并求其范圍即可
試題解析:
(Ⅰ)![]() .
.
因為![]() ,則
,則![]() 時
時![]() 時
時![]() ,
,
∴![]() 在
在![]() 上遞減,在
上遞減,在![]() 上遞增.
上遞增.
(Ⅱ)當![]() 時,若
時,若![]() ,則
,則![]() .
.
所以![]() 對任意的
對任意的![]() 恒成立 ,
恒成立 , ![]() .
.
由(Ⅰ)知,當![]() 時,
時, ![]() 在
在![]() 上遞減,在
上遞減,在![]() 上遞增.
上遞增.
依題意,有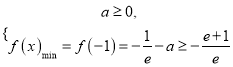 ,∴
,∴![]()
![]() .
.
∴![]() .
.
設![]() ,則
,則![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() 在
在![]() 上遞增,
上遞增,
∵![]() ,
, ![]() .
.
因此,存在唯一![]() ,使得
,使得![]() ,
,
當![]() 時,
時, ![]() ,
, ![]() ,
, ![]() 單調遞增;
單調遞增;
當![]() 時,
時, ![]() ,
, ![]() ,
, ![]() 單調遞減.
單調遞減.
因此![]() 在
在![]() 處取得最大值,最大值為
處取得最大值,最大值為
![]() ,
, ![]()
設![]() ,則
,則![]() ,
,
∴![]() 在
在![]() 上遞減,∴
上遞減,∴![]() ,∴
,∴![]()
∴![]() 時
時![]() 的最大值
的最大值![]() .
.
反之,任取![]() ,下證
,下證![]() ,
, ![]()
∵![]() 在
在![]() 上遞減,在
上遞減,在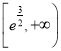 上遞增,且
上遞增,且![]() 時
時![]() ,
,
∴任取![]() ,存在唯一的
,存在唯一的![]() ,使得
,使得![]() .
.
∵![]() ,∴
,∴![]() 在
在![]() 上遞減,
上遞減,
∴![]() 時,
時, ![]() .
.
綜上,當![]() 對任意的
對任意的![]() 恒成立時,函數
恒成立時,函數![]() 最大值,最大值的取值范圍為
最大值,最大值的取值范圍為![]() .
.
注:后半部分的證明是為了說明當![]() 在
在![]() 內變化時, 能取遍
內變化時, 能取遍![]() 內的所有值,從而
內的所有值,從而![]() 的最大值能取遍
的最大值能取遍![]() 內所有的值,防止把
內所有的值,防止把![]() 的最大值的取值范圍變大.
的最大值的取值范圍變大.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】如圖,在正方體ABCD﹣A1B1C1D1中,E、F分別為棱AB、AD的中點.
(1)求證:EF平行平面CB1D1;
(2)求證:平面CAA1C1⊥平面CB1D1
(3)求直線A1C與平面ABCD所成角的正切值.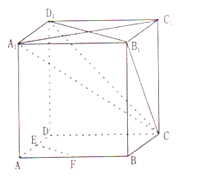
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某紡紗廠生產甲、乙兩種棉紗,已知生產甲種棉紗1噸需耗一級籽棉2噸、二級籽棉1噸;生產乙種棉紗1噸需耗一級籽棉1噸,二級籽棉2噸.每1噸甲種棉紗的利潤為900元,每1噸乙種棉紗的利潤為600元.工廠在生產這兩種棉紗的計劃中,要求消耗一級籽棉不超過250噸,二級籽棉不超過300噸.問甲、乙兩種棉紗應各生產多少噸,能使利潤總額最大?并求出利潤總額的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】酒后違法駕駛機動車危害巨大,假設駕駛人員血液中的酒精含量為![]() (簡稱血酒含量,單位是毫克/100毫升),當
(簡稱血酒含量,單位是毫克/100毫升),當![]() 時,為酒后駕車;當
時,為酒后駕車;當![]() 時,為醉酒駕車.如圖為某市交管部分在一次夜間行動中依法查出的
時,為醉酒駕車.如圖為某市交管部分在一次夜間行動中依法查出的![]() 名飲酒后違法駕駛機動車者抽血檢測后所得頻率分布直方圖(其中
名飲酒后違法駕駛機動車者抽血檢測后所得頻率分布直方圖(其中![]() 人數包含
人數包含![]() ).
).
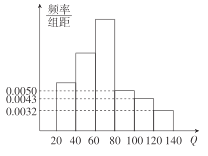
(Ⅰ)求查獲的醉酒駕車的人數;
(Ⅱ)從違法駕車的![]() 人中按酒后駕車和醉酒駕車利用分層抽樣抽取
人中按酒后駕車和醉酒駕車利用分層抽樣抽取![]() 人做樣本進行研究,再從抽取的
人做樣本進行研究,再從抽取的![]() 人中任取
人中任取![]() 人,求
人,求![]() 人中含有醉酒駕車人數
人中含有醉酒駕車人數![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】 (本小題滿分12分)
如圖, 在四面體ABOC中, ![]() , 且
, 且![]() .
.
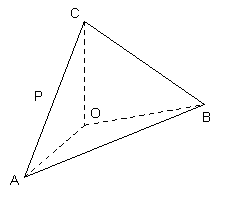
(Ⅰ)設為![]() 為
為![]() 的中點, 證明: 在
的中點, 證明: 在![]() 上存在一點
上存在一點![]() ,使
,使![]() ,并計算
,并計算![]() ;
;
(Ⅱ)求二面角![]() 的平面角的余弦值。
的平面角的余弦值。
查看答案和解析>>
科目:高中數學 來源: 題型:
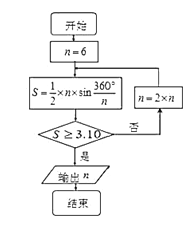
【題目】公元263年左右,我國數學家劉徽發現當圓內接正多邊形的邊數無限增加時,多邊形面積可無限逼近圓的面積,并創立了“割圓術”,利用“割圓術”劉徽得到了圓周率精確到小數點后兩位的近似值![]() ,這就是著名的“徽率”,如圖是利用劉徽的“割圓術”思想設計的一個程序框圖,則輸出
,這就是著名的“徽率”,如圖是利用劉徽的“割圓術”思想設計的一個程序框圖,則輸出![]() 的值為 ( )
的值為 ( )
(參考數據:![]() )
)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
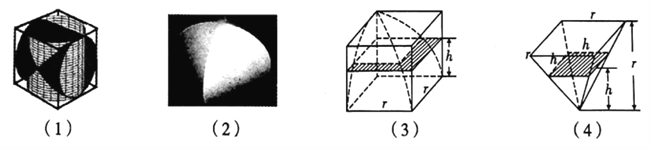
【題目】中國古代數學家劉徽在《九章算術注》中,稱一個正方體內兩個互相垂直的內切圓柱所圍成的立體為“牟合方蓋”,如圖(1)(2),劉徽未能求得牟合方蓋的體積,直言“欲陋形措意,懼失正理”,不得不說“敢不闕疑,以俟能言者”.約200年后,祖沖之的兒子祖暅提出“冪勢既同,則積不容異”,后世稱為祖暅原理,即:兩等高立體,若在每一等高處的截面積都相等,則兩立體體積相等.如圖(3)(4),祖暅利用八分之一正方體去掉八分之一牟合方蓋后的幾何體與長寬高皆為八分之一正方體的邊長的倒四棱錐“等冪等積”,計算出牟合方蓋的體積,據此可知,牟合方蓋的體積與其外切正方體的體積之比為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com