
對任意實數列 ,定義
,定義 它的第
它的第 項為
項為
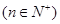 ,假設
,假設 是首項是
是首項是 公比為
公比為 的等比數列.
的等比數列.
(1)求數列 的前
的前 項和
項和 ;
;
(2)若 ,
, ,
, .
.
①求實數列 的通項
的通項 ;
;
②證明: .
.
(1) ;(2)①
;(2)① ;②詳見解析.
;②詳見解析.
解析試題分析:本題以新定義的模式考察了等比數列的通項公式和前n項和以及不等式的放縮法.(1)由 是首項是
是首項是 公比為
公比為 的等比數列,故實數列
的等比數列,故實數列 確定,即
確定,即
 ,再結合
,再結合 的定義,得
的定義,得 ,然后求和即可(需分類討論);(2)由
,然后求和即可(需分類討論);(2)由 ,
, .,可確定
.,可確定 ,利用累加法可求
,利用累加法可求 ;和式
;和式 可看作數列
可看作數列 的前n項和,故先求其通項公式,得
的前n項和,故先求其通項公式,得 ,因前n項和不易直接求出,故可考慮放縮法,首先看不等式右邊,可想到證明每項都小于
,因前n項和不易直接求出,故可考慮放縮法,首先看不等式右邊,可想到證明每項都小于 ,由
,由 ,進而可證明右面不等式,再考慮不等式左邊,
,進而可證明右面不等式,再考慮不等式左邊, ,因為
,因為
 ,故
,故 ,進而求和可證明.
,進而求和可證明.
試題解析:(1)令 這里
這里

 是公比為
是公比為 的等比數列.
的等比數列.


 ,
,
當 時,
時, ,
,
 ,. 2分
,. 2分
當 時,
時, 是公比為
是公比為 ,首項為
,首項為 的等比數列;.
的等比數列;. . 4分
. 4分 綜上
綜上
 . 6分
. 6分
(2)①由題設 ,
,
 ,
,
 疊加可得
疊加可得 (
( ). 8分
). 8分
②


 . 10分
. 10分
又

 ,
, ,
,
即 ,
,
 ,
,


 . 12分
. 12分

即 . 13分
. 13分
考點:1、等比數列通項公式;2、等比數列前n項和;3、累加法.


 同步輕松練習系列答案
同步輕松練習系列答案 課課通課程標準思維方法與能力訓練系列答案
課課通課程標準思維方法與能力訓練系列答案科目:高中數學 來源: 題型:解答題
等比數列{an}中,a1,a2,a3分別是下表第一、二、三行中的某一個數,且a1,a2,a3中的任何兩個數不在下表的同一列.
(1)求數列{an}的通項公式;
(2)若數列{bn}滿足:bn=an+(-1)nlnan,求數列{bn}的前n項和Sn·
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知數列{an}的各項均為正數的等比數列,且a1a2=2,a3a4=32,
(1)求數列{an}的通項公式;
(2)設數列{bn}的前n項和為Sn=n2,(n∈N*),求數列{anbn}的前n項和Tn.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知數列{an}成等比數列,且an>0.
(1)若a2-a1=8,a3=m.①當m=48時,求數列{an}的通項公式;②若數列{an}是唯一的,求m的值;
(2)若a2k+a2k-1+…+ak+1-(ak+ak-1+…+a1)=8,k∈N*,求a2k+1+a2k+2+…+a3k的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com