日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

精英家教網 > 高中數學 > 題目詳情

設平面向量a="(x1,y1),b=(x2,y2)" ,定義運算⊙：a⊙b ="x1y2-y1x2" .已知平面向量a，b，c，則下列說法錯誤的是


  1. A.
    (a⊙b)+(b⊙a)=0
  2. B.
    存在非零向量a，b同時滿足a⊙b=0且a?b=0
  3. C.
    (a+b)⊙c=(a⊙c)+(b⊙c)
  4. D.
    |a⊙b|2= |a|2|b|2-|a?b|2
B
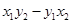
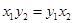
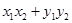
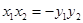
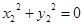
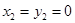
由題干定義知：a⊙b==0，得 （1），由a?b==0得 (2) ,由(1)/(2)得,故，與向量b非零矛盾，故選B
練習冊系列答案
相關習題

科目：高中數學 來源： 題型：

設平面向量
a
=（cosx，sinx），
b
=(cosx+2
3
，sinx)，
c
=(sinα，cosα)，x∈R，
（Ⅰ）若
a
⊥
c
，求cos（2x+2α）的值；
（Ⅱ）若x∈(0，
π
2
)，證明
a
和
b
不可能平行；
（Ⅲ）若α=0，求函數f(x)=
a
•(
b
-2
c
)的最大值，并求出相應的x值．

查看答案和解析>>

科目：高中數學 來源： 題型：

設平面向量
a
=(coxx，sinx)，
b
=(
3
2
，
1
2
)，函數f（x）=
a
•
b
+1．求：
①求函數f（x）的值域；
②求函數f（x）的單調增區間．

查看答案和解析>>

科目：高中數學 來源： 題型：

設平面向量
a
=（cosx，sinx），
b
=（cosx+2
3
，sinx），x∈R，
（1）若x∈（0，
π
2
），證明：
a
和
b
不可能平行；
（2）若
c
=（0，1），求函數f（x）=
a
•（
b
-2
c
）的最大值，并求出相應的x值．

查看答案和解析>>

科目：高中數學 來源： 題型：

（2014•瀘州一模）設平面向量
a
=（
3
sinx，2cosx），
b
=（2sin（
π
2
-x），cosx），已知f（x）=
a
•
b
+m在[0，
π
2
]上的最大值為6．
（Ⅰ）求實數m的值；
（Ⅱ）若f(
π
2
+x0)=
14
5
，x0∈[
π
4
，
π
2
]．求cos2x0的值．

查看答案和解析>>

科目：高中數學 來源： 題型：

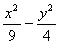
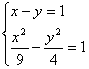
設平面向量a=(x，y)，b=(x2，y2)，c=(1，-1)，d=(，-)，若a·c=b·d=1，則這樣的向量a的個數是(    )

A.0                    B.1                     C.2                    D.4

查看答案和解析>>

同步練習冊答案
主站蜘蛛池模板： 欧美日韩亚洲国内综合网 | 精品国产一区二区在线 | 国产第一夜| 国产激情在线观看视频 | 国产成人精品午夜在线播放 | 国产羞羞视频 | 日本一区二区三区视频在线观看 | 99精品福利视频 | 日批在线观看 | 精品国产一区二区三区性色av | 北条麻妃国产九九九精品小说 | 久久精品视频7 | 在线看av网址 | 国产精品久久91 | 国产精品久久九九 | 亚洲高清在线观看 | 成人亚洲区 | 日韩免费福利视频 | 99久久婷婷国产精品综合 | 成人国产精品视频 | 羞羞视频网站免费看 | 亚洲一区中文字幕永久在线 | 日本在线三级 | 九九久久国产 | 天天射欧美 | 国产亚洲精品久久久久动 | 久久国产传媒 | 日日干天天操 | 91九色最新| 中文字幕av高清 | 亚洲激情第一页 | 久草操 | 天堂福利影院 | 久久久久国产一级毛片高清版小说 | 另类免费视频 | 国产一区二区视频精品 | 免费久久精品 | 日韩一区二区三区在线视频 | 成人免费一区二区三区视频网站 | 操视频网站 | 国产亚洲综合一区二区 |