
【題目】某市場調查發現,某種產品在投放市場的30天中,其銷售價格![]() (元)和時間
(元)和時間![]() (天)(
(天)(![]() )的關系如圖所示
)的關系如圖所示
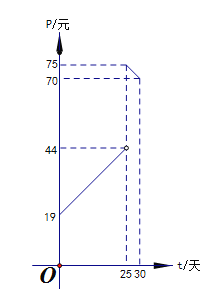
(1)寫出銷售價格![]() (元)和時間
(元)和時間![]() (天)的函數解析式;
(天)的函數解析式;
(2)若日銷售量![]() (件)與時間
(件)與時間![]() (天)的函數關系是
(天)的函數關系是![]() (
(![]() ,
,![]() ),求該商品的日銷售金額
),求該商品的日銷售金額![]() (元)與時間
(元)與時間![]() (天)的函數解析式;
(天)的函數解析式;
(3)問該產品投放市場第幾天時,日銷售金額最高?最高值為多少元?
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的長軸長為
的長軸長為![]() ,焦距為2,拋物線
,焦距為2,拋物線![]() 的準線經過C的左焦點F.
的準線經過C的左焦點F.
(1)求C與M的方程;
(2)直線l經過C的上頂點且l與M交于P,Q兩點,直線FP,FQ與M分別交于點D(異于點P),E(異于點Q),證明:直線DE的斜率為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 過點
過點![]() ,過坐標原點
,過坐標原點![]() 作兩條互相垂直的射線與橢圓
作兩條互相垂直的射線與橢圓![]() 分別交于
分別交于![]() ,
,![]() 兩點.
兩點.
(1)證明:當![]() 取得最小值時,橢圓
取得最小值時,橢圓![]() 的離心率為
的離心率為![]() .
.
(2)若橢圓![]() 的焦距為2,是否存在定圓與直線
的焦距為2,是否存在定圓與直線![]() 總相切?若存在,求定圓的方程;若不存在,請說明理由.
總相切?若存在,求定圓的方程;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地環保部門跟蹤調查一種有害昆蟲的數量.根據調查數據,該昆蟲的數量![]() (萬只)與時間
(萬只)與時間![]() (年)(其中
(年)(其中![]() )的關系為
)的關系為![]() .為有效控制有害昆蟲數量、保護生態環境,環保部門通過實時監控比值
.為有效控制有害昆蟲數量、保護生態環境,環保部門通過實時監控比值![]() (其中
(其中![]() 為常數,且
為常數,且![]() )來進行生態環境分析.
)來進行生態環境分析.
(1)當![]() 時,求比值
時,求比值![]() 取最小值時
取最小值時![]() 的值;
的值;
(2)經過調查,環保部門發現:當比值![]() 不超過
不超過![]() 時不需要進行環境防護.為確保恰好3年不需要進行保護,求實數
時不需要進行環境防護.為確保恰好3年不需要進行保護,求實數![]() 的取值范圍.(
的取值范圍.(![]() 為自然對數的底,
為自然對數的底, ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知扇形![]() 是一個觀光區的平面示意圖,其中扇形半徑為10米,
是一個觀光區的平面示意圖,其中扇形半徑為10米,![]() ,為了便于游客觀光和旅游,提出以下兩種設計方案:
,為了便于游客觀光和旅游,提出以下兩種設計方案:
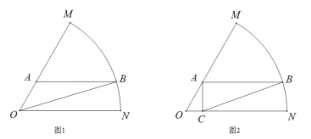
(1)如圖1,擬在觀光區內規劃一條三角形![]() 形狀的道路,道路的一個頂點
形狀的道路,道路的一個頂點![]() 在弧
在弧![]() 上,另一頂點
上,另一頂點![]() 在半徑
在半徑![]() 上,且
上,且![]() ,求
,求![]() 周長的最大值;
周長的最大值;
(2)如圖2,擬在觀光區內規劃一個三角形區域種植花卉,三角形花圃![]() 的一個頂點
的一個頂點![]() 在弧
在弧![]() 上,另兩個頂點
上,另兩個頂點![]()
![]() 在半徑
在半徑![]()
![]() 上,且
上,且![]() ,
,![]() ,求花圃
,求花圃![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() 的離心率為
的離心率為![]() ,過焦點且與
,過焦點且與![]() 軸垂直的直線被橢圓
軸垂直的直線被橢圓![]() 截得的線段長為
截得的線段長為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)已知點![]() ,
,![]() ,過點
,過點![]() 的任意一條直線
的任意一條直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
,![]() 兩點,求證:
兩點,求證:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某廠生產某產品的年固定成本為250萬元,每生產![]() 千件,需另投入成本
千件,需另投入成本![]() (萬元),若年產量不足
(萬元),若年產量不足![]() 千件,
千件, ![]() 的圖像是如圖的拋物線,此時
的圖像是如圖的拋物線,此時![]() 的解集為
的解集為![]() ,且
,且![]() 的最小值是
的最小值是![]() ,若年產量不小于
,若年產量不小于![]() 千件,
千件, ![]() ,每千件商品售價為50萬元,通過市場分析,該廠生產的商品能全部售完;
,每千件商品售價為50萬元,通過市場分析,該廠生產的商品能全部售完;
(1)寫出年利潤![]() (萬元)關于年產量
(萬元)關于年產量![]() (千件)的函數解析式;
(千件)的函數解析式;
(2)年產量為多少千件時,該廠在這一商品的生產中所獲利潤最大?

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,直三棱柱![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 是
是![]() 的中點,△
的中點,△![]() 是等腰三角形,
是等腰三角形, ![]() 為
為![]() 的中點,
的中點, ![]() 為
為![]() 上一點;
上一點;
(1)若![]() ∥平面
∥平面![]() ,求
,求![]() ;
;
(2)平面![]() 將三棱柱
將三棱柱![]() 分成兩個部分,求含有點
分成兩個部分,求含有點![]() 的那部分體積;
的那部分體積;
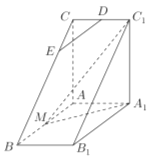
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近來天氣變化無常,陡然升溫、降溫幅度大于![]() 的天氣現象出現增多.陡然降溫幅度大于
的天氣現象出現增多.陡然降溫幅度大于![]() 容易引起幼兒傷風感冒疾病.為了解傷風感冒疾病是否與性別有關,在某婦幼保健院隨機對人院的
容易引起幼兒傷風感冒疾病.為了解傷風感冒疾病是否與性別有關,在某婦幼保健院隨機對人院的![]() 名幼兒進行調查,得到了如下的列聯表,若在全部
名幼兒進行調查,得到了如下的列聯表,若在全部![]() 名幼兒中隨機抽取
名幼兒中隨機抽取![]() 人,抽到患傷風感冒疾病的幼兒的概率為
人,抽到患傷風感冒疾病的幼兒的概率為![]() ,
,
(1)請將下面的列聯表補充完整;
患傷風感冒疾病 | 不患傷風感冒疾病 | 合計 | |
男 | 25 | ||
女 | 20 | ||
合計 | 100 |
(2)能否在犯錯誤的概率不超過![]() 的情況下認為患傷風感冒疾病與性別有關?說明你的理由;
的情況下認為患傷風感冒疾病與性別有關?說明你的理由;
(3)已知在患傷風感冒疾病的![]() 名女性幼兒中,有
名女性幼兒中,有![]() 名又患黃痘病.現在從患傷風感冒疾病的
名又患黃痘病.現在從患傷風感冒疾病的![]() 名女性中,選出
名女性中,選出![]() 名進行其他方面的排查,記選出患黃痘病的女性人數為
名進行其他方面的排查,記選出患黃痘病的女性人數為![]() ,求
,求![]() 的分布列以及數學期望.下面的臨界值表供參考:
的分布列以及數學期望.下面的臨界值表供參考:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
參考公式: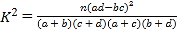 ,其中
,其中![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com