
計算:(1)lg32+lg35+3lg 2·lg 5;
(2)已知loga2=m,loga3=n,求a2m+n的值;
(3)已知10a=2,10b=3,求1002a-b的值.
解:(1)lg32+lg35+3lg 2·lg 5
=(lg 2+lg 5)(lg22-lg 2·lg 5+lg25)+3lg 2·lg 5
=lg 10[(lg 2+lg 5)2-3lg 2·lg 5]+3lg 2·lg 5
=1.
∵loga2=m,∴am=2.
∵loga3=n,∴an=3.
方法1:故a2m+n=(am)2·an=4×3=12.
方法2:∵loga2=m,loga3=n,
![]()
(3)方法1:∵10a=2,∴lg 2=a.
∵10b=3,∴lg 3=b.
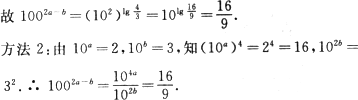
分析:(1)由式子結構想到立方和公式a3+b3=(a+b)(a2-ab+b2).
(2)、(3)小題可以根據式子結構特征,將已知式子變式,再代入求值.
解題心得:(1)利用對數的運算性質計算時,常將式子化為含有lg 2+lg 5(=1)的式子,解題中應靈活運用有關乘法公式.
(2)注意解題中整體代換,如lg 2+lg 5可用1替代等.


科目:高中數學 來源: 題型:
| 3 |
| 2 |
| 3 |
| 8 |
| 1 |
| 3 |
| 2 |
| 3 |
| 4 | 3
| |||
查看答案和解析>>
科目:高中數學 來源: 題型:
| 3 | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 2 |
| 3 |
| 1 |
| 2 |
| 16 |
| 81 |
| 3 |
| 4 |
| lg2+lg5-lg1 | ||
2lg
|
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com