
如圖, 在平面
在平面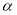 內,
內, ,
, ,P為平面
,P為平面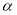 外一個動點,且PC=
外一個動點,且PC= ,
,

(1)問當PA的長為多少時,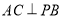
(2)當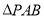 的面積取得最大值時,求直線BC與平面PAB所成角的大小
的面積取得最大值時,求直線BC與平面PAB所成角的大小
(1)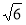 ;(2)
;(2)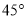
【解析】
試題分析:(1)由分析可知當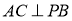 時,
時,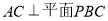 ,則
,則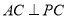 ,由勾股定理可求得
,由勾股定理可求得 。(2)因為
。(2)因為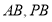 為定值,且
為定值,且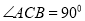 ,
,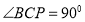 ,所以當
,所以當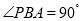 時,
時,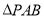 的面積取得最大值。分析可知
的面積取得最大值。分析可知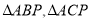 均是以
均是以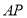 為底的等腰三角形,故取
為底的等腰三角形,故取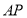 中點
中點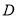 ,連接
,連接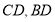 。則有
。則有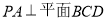 ,從而可得
,從而可得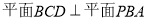 ,可知
,可知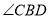 就是直線
就是直線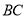 與平面PAB所成角,在
與平面PAB所成角,在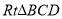 中可求此角。
中可求此角。
試題解析:(1)因為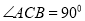 ,所以
,所以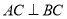 ,當
,當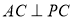 時,
時,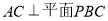 ,而
,而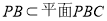 ,所以
,所以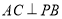 ,此時,
,此時,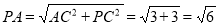 ,即當PA=
,即當PA=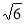 時,
時,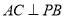
(2)
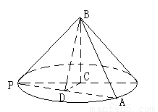
在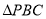 中,因為PC=
中,因為PC=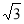 ,
,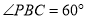 ,
,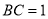 ,所以
,所以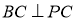 ,當
,當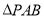 的面積取得最大值時,
的面積取得最大值時,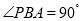 ,(如圖)在
,(如圖)在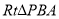 中,因為
中,因為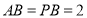 ,取
,取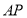 中點
中點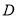 ,連接
,連接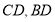 。則
。則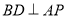 ,因為
,因為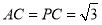 且點
且點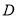 為
為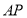 中點,所以
中點,所以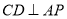 ,因為
,因為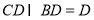 ,所以
,所以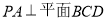 ,由此可求得
,由此可求得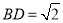 ,又在
,又在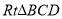 中,
中,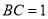 ,所以
,所以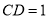 ,由于
,由于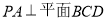 ,所以
,所以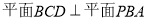 ,所以
,所以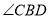 就是直線
就是直線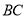 與平面PAB所成角,在
與平面PAB所成角,在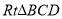 中,因為
中,因為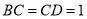 ,所以
,所以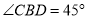 ,所以直線BC與平面
,所以直線BC與平面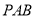 所成角的大小為
所成角的大小為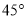
考點:1線線垂直、線面垂直;2線面角。


 鴻圖圖書寒假作業假期作業吉林大學出版社系列答案
鴻圖圖書寒假作業假期作業吉林大學出版社系列答案科目:高中數學 來源:2013-2014學年湖北省天門市畢業生四月調研考試文科數學試卷(解析版) 題型:選擇題
下圖是根據變量x,y的觀測數據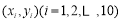 得到的散點圖,由這些散點圖可以判斷變量x,y具有相關關系的圖是( )
得到的散點圖,由這些散點圖可以判斷變量x,y具有相關關系的圖是( )
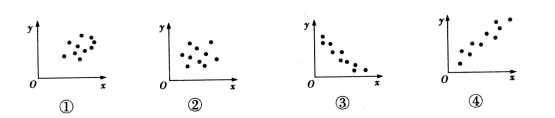
A.①② B.①④ C.②③ D.③④
查看答案和解析>>
科目:高中數學 來源:2013-2014學年湖北省七市(州)高三年級聯合考試文科數學試卷(解析版) 題型:選擇題
萊因德紙草書》是世界上最古老的數學著作之一,書中有這樣的一道題目:把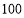 個面包分給
個面包分給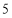 個人,使每人所得成等差數列,且使較大的三份之和的
個人,使每人所得成等差數列,且使較大的三份之和的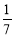 是較小的兩份之和,則最小的
是較小的兩份之和,則最小的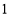 份為( )
份為( )
A.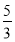 B.
B.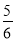 C.
C.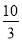 D.
D.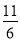
查看答案和解析>>
科目:高中數學 來源:2013-2014學年浙江省高三高考模擬沖刺卷(提優卷)(二)理科數學試卷(解析版) 題型:選擇題
正四面體ABCD,線段AB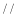 平面
平面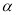 ,E,F分別是線段AD和BC的中點,當正四面體繞以AB為軸旋轉時,則線段AB與EF在平面
,E,F分別是線段AD和BC的中點,當正四面體繞以AB為軸旋轉時,則線段AB與EF在平面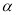 上的射影所成角余弦值的范圍是( )
上的射影所成角余弦值的范圍是( )
A. [0,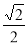 ] B.[
] B.[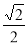 ,1] C.[
,1] C.[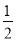 ,1] D.[
,1] D.[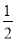 ,
,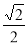 ]
]
查看答案和解析>>
科目:高中數學 來源:2013-2014學年浙江省高三高考模擬沖刺卷(提優卷)(二)理科數學試卷(解析版) 題型:選擇題
設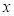 為非零實數,則p:
為非零實數,則p: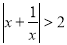 是q:
是q: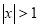 成立的 ( )
成立的 ( )
A.充分不必要條件 B.必要不充分條件
C.充分必要條件 D.既不充分也不必要條件
查看答案和解析>>
科目:高中數學 來源:2013-2014學年浙江省高三高考模擬沖刺卷(提優卷)(二)文科數學試卷(解析版) 題型:選擇題
若實數x,y滿足: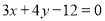 ,則
,則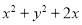 的最小值是( )
的最小值是( )
A.2 B.3 C.5 D.8
查看答案和解析>>
科目:高中數學 來源:2013-2014學年浙江省高三高考模擬沖刺卷(提優卷)(三)理科數學試卷(解析版) 題型:填空題
已知PA垂直于正方形ABCD所在平面,連接PB、PC、PD、AC、BD,則下列垂直關系中正確的序號是 .
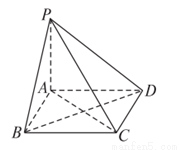
①平面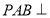 平面PBC ②平面
平面PBC ②平面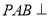 平面PAD ③平面
平面PAD ③平面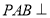 平面PCD
平面PCD
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com