
分析 (Ⅰ)記“每箱水果不能上市銷售”為事件A,即兩箱都不合格,由對立事件的概率公式可知:P(A)=1-(1-$\frac{1}{9}$)(1-$\frac{1}{10}$)=$\frac{1}{5}$;
(Ⅱ)可知X的取值為:-120,-70,-20,30,80,然后根據n次獨立重復試驗中恰好發生k次的概率公式分別求出相應的概率,列出分布列,最后根據數學期望公式解之即可.
解答 解:(Ⅰ)記“每箱水果不能上市銷售”為事件A,即兩箱都不合格,
由對立事件的概率公式可知:P(A)=1-(1-$\frac{1}{9}$)(1-$\frac{1}{10}$)=$\frac{1}{5}$,
所以每箱水果不能上市銷售的概率為$\frac{1}{5}$.…(3分)
(Ⅱ)由已知,可知X的取值為:-120,-70,-20,30,80.…(4分)
P(X=-120)=${C}_{4}^{4}$($\frac{1}{5}$)4($\frac{4}{5}$)0=$\frac{1}{625}$,
P(X=-70)=${C}_{4}^{3}$($\frac{1}{5}$)3($\frac{4}{5}$)1=$\frac{16}{625}$,
P(X=-20)=${C}_{4}^{2}$($\frac{1}{5}$)2($\frac{4}{5}$)2=$\frac{96}{625}$,
P(X=30)=${C}_{4}^{1}$($\frac{1}{5}$)1($\frac{4}{5}$)3=$\frac{256}{625}$,
P(X=80)=${C}_{4}^{0}$($\frac{1}{5}$)0($\frac{4}{5}$)4=$\frac{256}{625}$.…(9分)
所以X的分布列為:
| X | -120 | -70 | -20 | 30 | 80 |
| P | $\frac{1}{625}$ | $\frac{16}{625}$ | $\frac{96}{625}$ | $\frac{256}{625}$ | $\frac{256}{625}$ |
點評 本題主要考查了n次獨立重復試驗中恰好發生k次的概率,以及離散型隨機變量的概率分別和數學期望,同時考查了計算能力,屬于中檔題.


 勵耘書業暑假銜接寧波出版社系列答案
勵耘書業暑假銜接寧波出版社系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | n+1 | B. | n | C. | n-1 | D. | n-2 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
| X | 0 | 1 | 2 | 3 |
| P | $\frac{1}{8}$ | $\frac{3}{8}$ | $\frac{3}{8}$ | a |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
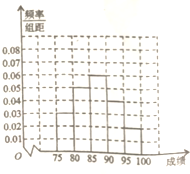 某高中畢業學年,在高校自主招生期間,把學生的平時成績按“百分制”折算,排出前100名學生,并對這100名學生按成績分組(從低到高依次分為第1組、第2組、第3組、第4組、第5組),其頻率分布直方圖如圖:現Q大學決定在第3、4、5組中用分層抽樣的方法抽取6名學生進行面試,且本次面試中有B、C、D三位考官.
某高中畢業學年,在高校自主招生期間,把學生的平時成績按“百分制”折算,排出前100名學生,并對這100名學生按成績分組(從低到高依次分為第1組、第2組、第3組、第4組、第5組),其頻率分布直方圖如圖:現Q大學決定在第3、4、5組中用分層抽樣的方法抽取6名學生進行面試,且本次面試中有B、C、D三位考官.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
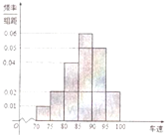 我州某高中一研究性學習小組,在某一告訴公路服務區進行社會實踐活動,從小型汽車中按進服務區的先后,每間隔5輛就抽取一輛的抽樣方法抽取40名駕駛員進行詢問調查,將他們在某段高速公路的車速(km/h)分成六段:[70,75),[75,80),[80,85),[85,90),[90,95),[95,100),統計后得到如圖的頻率分布直方圖.
我州某高中一研究性學習小組,在某一告訴公路服務區進行社會實踐活動,從小型汽車中按進服務區的先后,每間隔5輛就抽取一輛的抽樣方法抽取40名駕駛員進行詢問調查,將他們在某段高速公路的車速(km/h)分成六段:[70,75),[75,80),[80,85),[85,90),[90,95),[95,100),統計后得到如圖的頻率分布直方圖.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com