
【題目】已知定義在![]() 上的函數
上的函數![]() 的圖像關于直線
的圖像關于直線![]() 對稱,且當
對稱,且當![]() 時,
時,![]() ,過點
,過點![]() 作曲線
作曲線![]() 的兩條切線,若這兩條切線互相垂直,則該函數
的兩條切線,若這兩條切線互相垂直,則該函數![]() 的最小值為( )
的最小值為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
當![]() 時,
時,![]() ,可得函數
,可得函數![]() 在
在![]() 為增函數,結合函數的對稱性可得函數的最小值為
為增函數,結合函數的對稱性可得函數的最小值為![]() ,進而分析可得點
,進而分析可得點![]() 作曲線
作曲線![]() 的兩條切線的斜率
的兩條切線的斜率![]() ,設
,設![]() 右側的切點為
右側的切點為![]() ,求出函數的導數,由導數的幾何意義可得
,求出函數的導數,由導數的幾何意義可得![]() ,即
,即![]() ,結合兩點間連線的斜率公式可得
,結合兩點間連線的斜率公式可得![]() ,即
,即![]() ,聯立兩式求出
,聯立兩式求出![]() 的值,代入函數的解析式可得結果.
的值,代入函數的解析式可得結果.
根據題意,分析可得當![]() 時,
時,![]() ,
,
則函數![]() 在
在![]() 為增函數,
為增函數,
又由函數![]() 的圖象關于直線
的圖象關于直線![]() 對稱,函數
對稱,函數![]() 在
在![]() 為減函數,
為減函數,
所以函數的最小值為![]() ,
,
點![]() 作曲線
作曲線![]() 的兩條切線,
的兩條切線,
則兩條切線的關于直線![]() 對稱,即兩條切線的斜率互為相反數,
對稱,即兩條切線的斜率互為相反數,
若兩條切線互相垂直,切線的斜率![]() ,
,
設![]() 右側的切點為
右側的切點為![]() ,
,
因為![]() ,所以導數
,所以導數![]() ,
,
則有![]() ,即
,即![]() ,①
,①
又由切線過點![]() ,可得
,可得![]() ,
,
即![]() ,解可得
,解可得![]() ,②
,②
聯立①②可得![]() ,
,
則函數![]() 的最小值為
的最小值為![]() ,故選B.
,故選B.


科目:高中數學 來源: 題型:
【題目】已知n為給定的正整數,t為給定的實數,設(t+x)n=a0+a1x+a2x2+…+anxn.
(1)當n=8時.
①若t=1,求a0+a2+a4+a6+a8的值;
②若t=![]() ,求數列{an}中的最大值;
,求數列{an}中的最大值;
(2)若t=![]() ,當
,當![]() 時,求
時,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一湖中有不在同一直線的三個小島A、B、C,前期為開發旅游資源在A、B、C三島之間已經建有索道供游客觀賞,經測量可知AB兩島之間距離為3公里,BC兩島之間距離為5公里,AC兩島之間距離為7公里,現調查后發現,游客對在同一圓周上三島A、B、C且位于![]() (優弧)一片的風景更加喜歡,但由于環保、安全等其他原因,沒辦法盡可能一次游覽更大面積的湖面風光,現決定在
(優弧)一片的風景更加喜歡,但由于環保、安全等其他原因,沒辦法盡可能一次游覽更大面積的湖面風光,現決定在![]() 上選擇一個點D建立索道供游客游覽,經研究論證為使得游覽面積最大,只需使得△ADC面積最大即可.則當△ADC面積最大時建立索道AD的長為______公里.(注:索道兩端之間的長度視為線段)
上選擇一個點D建立索道供游客游覽,經研究論證為使得游覽面積最大,只需使得△ADC面積最大即可.則當△ADC面積最大時建立索道AD的長為______公里.(注:索道兩端之間的長度視為線段)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個正方形花圃被分成5份.
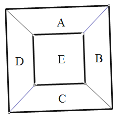
(1)若給這5個部分種植花,要求相鄰兩部分種植不同顏色的花,己知現有紅、黃、藍、綠4種顏色不同的花,求有多少種不同的種植方法?
(2)若將6個不同的盆栽都擺放入這5個部分,且要求每個部分至少有一個盆栽,問有多少種不同的放法?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列判斷正確的是( )
A.若隨機變量![]() 服從正態分布
服從正態分布![]() ,
,![]() ,則
,則![]() ;
;
B.已知直線![]() 平面
平面![]() ,直線
,直線![]() 平面
平面![]() ,則“
,則“![]() ”是“
”是“![]() ”的必要不充分條件;
”的必要不充分條件;
C.若隨機變量![]() 服從二項分布:
服從二項分布:![]() ,則
,則![]() ;
;
D.已知直線![]() 經過點
經過點![]() ,則
,則![]() 的取值范圍是
的取值范圍是![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某小型企業甲產品生產的投入成本x(單位:萬元)與產品銷售收入y(單位:萬元)存在較好的線性關系,下表記錄了最近5次該產品的相關數據.
x(萬元) | 3 | 5 | 7 | 9 | 11 |
y(萬元) | 8 | 10 | 13 | 17 | 22 |
(1)求y關于x的線性回歸方程;
(2)根據(1)中的回歸方程,判斷該企業甲產品投入成本12萬元的毛利率更大還是投入成本15萬元的毛利率更大(毛利率![]()
![]()
![]() )?
)?
相關公式: ,
,![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com