
 所確定的平面區域的面積為S=f(t),則S的最大值為________.
所確定的平面區域的面積為S=f(t),則S的最大值為________.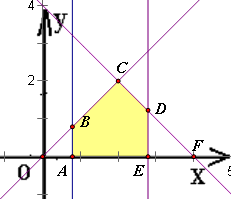 作出題中約束條件所確定的平面區域,如右圖陰影部分
作出題中約束條件所確定的平面區域,如右圖陰影部分 |OA|•|AB|=
|OA|•|AB|=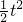 ,S△DEF=
,S△DEF= |DE|•|EF|=
|DE|•|EF|= (2-t)2,
(2-t)2, ×4×2-
×4×2-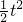 -
- (2-t)2=-t2+2t+2
(2-t)2=-t2+2t+2

 輕松暑假總復習系列答案
輕松暑假總復習系列答案科目:高中數學 來源:2012年河南省高考適應性考試數學模擬試卷(文科)(解析版) 題型:選擇題
 所確定的平面區域的面積為S=f(t),則S的最大值為( )
所確定的平面區域的面積為S=f(t),則S的最大值為( )查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com