
 的首項(xiàng)
的首項(xiàng) ,
, 是
是 的前
的前 項(xiàng)和,且
項(xiàng)和,且
 .
. ,求數(shù)列
,求數(shù)列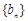 的通項(xiàng)公式;
的通項(xiàng)公式; ,證明:
,證明: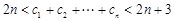 ,
, .
.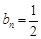 ;(2)詳見解析.
;(2)詳見解析.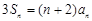 ,得:
,得: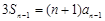
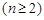 ,兩式相加,得:
,兩式相加,得: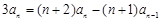 ,
,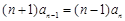
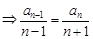 ,即
,即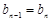 ,所以
,所以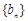 是常數(shù)列.又
是常數(shù)列.又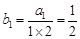 ,即可求出結(jié)果;(2)由(1)得
,即可求出結(jié)果;(2)由(1)得 ,進(jìn)而可求
,進(jìn)而可求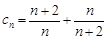 ,又
,又 ,所以
,所以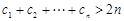 ;又由于
;又由于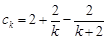 ,利于裂項(xiàng)相消法可求得
,利于裂項(xiàng)相消法可求得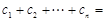
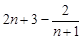
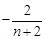 ,顯然可證右邊成立.
,顯然可證右邊成立.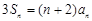 ,得:
,得: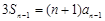
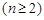 ,
,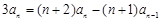 ,
,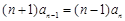
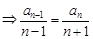
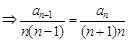 ,即
,即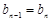 ,所以
,所以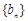 是常數(shù)列.
是常數(shù)列.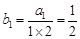 ,所以
,所以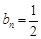 . .5分
. .5分 ,從而
,從而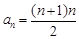 ,
,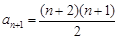 ,
, ,
,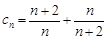 . .7分
. .7分 ,所以
,所以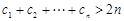 . 9分
. 9分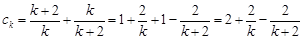 ,
,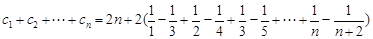
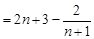
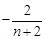
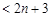 . .12分
. .12分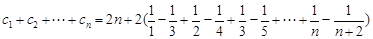
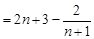
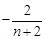 ,因?yàn)?img src="http://thumb.zyjl.cn/pic2/upload/papers/20140824/20140824052927507544.png" style="vertical-align:middle;" />
,因?yàn)?img src="http://thumb.zyjl.cn/pic2/upload/papers/20140824/20140824052927507544.png" style="vertical-align:middle;" />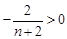 ,所以
,所以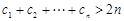 ).
).


| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
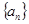 和
和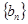 滿足
滿足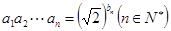 .若
.若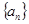 為等比數(shù)列,且
為等比數(shù)列,且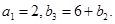
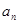 與
與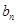 ;
;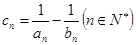 。記數(shù)列
。記數(shù)列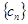 的前
的前 項(xiàng)和為
項(xiàng)和為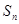 .
.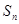 ;
;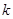 ,使得對任意
,使得對任意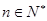 ,均有
,均有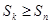 .
.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
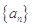 的首項(xiàng)
的首項(xiàng)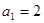 ,且對任意
,且對任意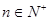 都有
都有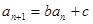 (其中
(其中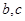 為常數(shù)).
為常數(shù)).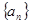 為等差數(shù)列,且
為等差數(shù)列,且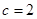 ,求
,求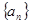 的通項(xiàng)公式.
的通項(xiàng)公式.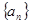 是等比數(shù)列,且
是等比數(shù)列,且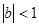 ,從數(shù)列
,從數(shù)列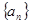 中任意取出相鄰的三項(xiàng),均能按某種順序排成等差數(shù)列,求
中任意取出相鄰的三項(xiàng),均能按某種順序排成等差數(shù)列,求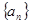 的前
的前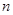 項(xiàng)和
項(xiàng)和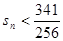 成立的
成立的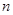 的取值的集合.
的取值的集合.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
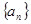 的各項(xiàng)均為正數(shù),且
的各項(xiàng)均為正數(shù),且
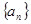 的通項(xiàng)公式;
的通項(xiàng)公式;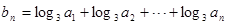 ,求數(shù)列
,求數(shù)列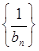 的前n項(xiàng)和
的前n項(xiàng)和 ;
;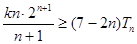 恒成立的實(shí)數(shù)
恒成立的實(shí)數(shù)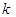 的取值范圍.
的取值范圍.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
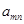 表示位于從上到下第
表示位于從上到下第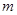 行,從左到右
行,從左到右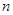 列的數(shù),比如
列的數(shù),比如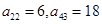 ,若
,若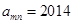 ,則有( )
,則有( )
A. | B. |
C.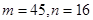 | D. |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
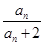 (n∈N*).若bn+1=(n-λ)(
(n∈N*).若bn+1=(n-λ)(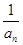 +1)(n∈N*),b1=-λ,且數(shù)列{bn}是單調(diào)遞增數(shù)列,則實(shí)數(shù)λ的取值范圍為( )
+1)(n∈N*),b1=-λ,且數(shù)列{bn}是單調(diào)遞增數(shù)列,則實(shí)數(shù)λ的取值范圍為( )| A.λ>2 | B.λ>3 | C.λ<2 | D.λ<3 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com