
【題目】某企業為了增加某種產品的生產能力,提出甲、乙兩個方案。甲方案是廢除原有生產線并引進一條新生產線,需一次性投資1000萬元,年生產能力為300噸;乙方案是改造原有生產線,需一次性投資700萬元,年生產能力為200噸;根據市場調查與預測,該產品的年銷售量的頻率分布直方圖如圖所示,無論是引進新生產線還是改造原有生產線,設備的使用年限均為6年,該產品的銷售利潤為1.5萬元/噸。
(Ⅰ)根據年銷售量的頻率分布直方圖,估算年銷量的平均數![]() (同一組中的數據用該組區間的中點值作代表);
(同一組中的數據用該組區間的中點值作代表);
(Ⅱ)將年銷售量落入各組的頻率視為概率,各組的年銷售量用該組區間的中點值作年銷量的估計值,并假設每年的銷售量相互獨立。
(i)根據頻率分布直方圖估計年銷售利潤不低于270萬的概率;
(ii)以企業6年的凈利潤的期望值作為決策的依據,試判斷該企業應選擇哪個方案。(6年的凈利潤=6年銷售利潤-投資費用)

【答案】(Ⅰ)206(Ⅱ) (ⅰ)0.7(ⅱ)乙方案
【解析】
(Ⅰ)由頻率分布直方圖能求出年銷量的平均數.
(Ⅱ)(i)該產品的銷售利潤為1.5萬元/噸,由頻率分布直方圖得只有當年平均銷量不低于180噸時年銷售利潤才不低于270萬,由此能求出年銷售利潤不低于270萬的概率.
(ii)分別求出甲方案6年的凈利潤的期望值和乙方案6年的凈利潤的期望值,由乙方案的凈利潤的期望值大于甲方案的凈利潤的期望值,得企業應該選擇乙方案.
(Ⅰ)年銷售量的平均數![]() (噸)
(噸)
(Ⅱ)(ⅰ)該產品的銷售利潤為![]() 萬元/噸,由直方圖可知只有當年平均銷量不低于
萬元/噸,由直方圖可知只有當年平均銷量不低于![]() 噸時,年銷售利潤才不低于
噸時,年銷售利潤才不低于![]() 萬,
萬,![]() 年銷售利潤不低于
年銷售利潤不低于![]() 萬的概率
萬的概率![]()
(ⅱ)設甲方案的年銷售量為![]() 噸,由(Ⅰ)可知甲方案的年銷售量的期望
噸,由(Ⅰ)可知甲方案的年銷售量的期望![]() ,
,
所以甲方案6年的凈利潤的期望值為:![]() (萬元)
(萬元)
設乙方案的年銷售量為![]() 噸,則乙方案的年銷售量的分布列為:
噸,則乙方案的年銷售量的分布列為:
|
|
|
|
|
|
|
|
![]() 乙方案的年銷售量期望
乙方案的年銷售量期望![]()
![]() 乙方案6年的凈利潤的期望值為:
乙方案6年的凈利潤的期望值為:![]() (萬元)
(萬元)
由上可知乙方案的凈利潤的期望值大于甲方案的凈利潤的期望值,故企業應選擇乙方案。


 備戰中考寒假系列答案
備戰中考寒假系列答案科目:高中數學 來源: 題型:
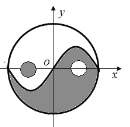
【題目】太極是中國古代的哲學術語,意為派生萬物的本源.太極圖是以黑白兩個魚形紋組成的圓形圖案,俗稱陰陽魚.太極圖形象化地表達了陰陽輪轉,相反相成是萬物生成變化根源的哲理.太極圖形展現了一種互相轉化,相對統一的形式美.按照太極圖的構圖方法,在平面直角坐標系中,圓![]() 被
被![]() 的圖象分割為兩個對稱的魚形圖案,圖中的兩個一黑一白的小圓通常稱為“魚眼”,已知小圓的半徑均為
的圖象分割為兩個對稱的魚形圖案,圖中的兩個一黑一白的小圓通常稱為“魚眼”,已知小圓的半徑均為![]() ,現在大圓內隨機投放一點,則此點投放到“魚眼”部分的概率為( )
,現在大圓內隨機投放一點,則此點投放到“魚眼”部分的概率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】古希臘時期,人們認為最美人體的頭頂至肚臍的長度與肚臍至足底的長度之比是![]() (
(![]() ≈0.618,稱為黃金分割比例),著名的“斷臂維納斯”便是如此.此外,最美人體的頭頂至咽喉的長度與咽喉至肚臍的長度之比也是
≈0.618,稱為黃金分割比例),著名的“斷臂維納斯”便是如此.此外,最美人體的頭頂至咽喉的長度與咽喉至肚臍的長度之比也是![]() .若某人滿足上述兩個黃金分割比例,且腿長為105cm,頭頂至脖子下端的長度為26 cm,則其身高可能是
.若某人滿足上述兩個黃金分割比例,且腿長為105cm,頭頂至脖子下端的長度為26 cm,則其身高可能是

A. 165 cmB. 175 cmC. 185 cmD. 190cm
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在三棱錐S-ABC中,已知SC⊥平面ABC,AB=BC=CA![]() ,SC=2,D、E分別為AB、BC的中點.若點P在SE上移動,求△PCD面積的最小值.
,SC=2,D、E分別為AB、BC的中點.若點P在SE上移動,求△PCD面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C的兩個焦點分別為F1(-1,0)、F2(1,0),短軸的兩個端點分別為B1,B2
(1)若△F1B1B2為等邊三角形,求橢圓C的方程;
(2)若橢圓C的短軸長為2,過點F2的直線l與橢圓C相交于P,Q兩點,且![]() ,求直線l的方程.
,求直線l的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com