
已知橢圓方程為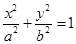 (
(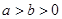 ),F
),F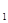 (-c,0)和F
(-c,0)和F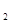 (c,0)分別是橢圓的左 右焦點.
(c,0)分別是橢圓的左 右焦點.
①若P是橢圓上的動點,延長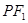 到M,使
到M,使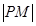 =
=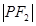 ,則M的軌跡是圓;
,則M的軌跡是圓;
②若P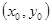 是橢圓上的動點,則
是橢圓上的動點,則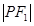
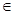
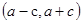 ;
;
③以焦點半徑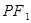 為直徑的圓必與以長軸為直徑的圓內切;
為直徑的圓必與以長軸為直徑的圓內切;
④若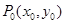 在橢圓
在橢圓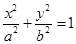 上,則過
上,則過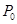 的橢圓的切線方程是
的橢圓的切線方程是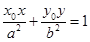 ;
;
⑤點P為橢圓上任意一點 ,則橢圓的焦點角形的面積為
,則橢圓的焦點角形的面積為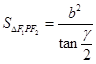 .
.
以上說法中,正確的有
①③④
解析試題分析:根據已知中橢圓方程為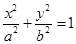 (
(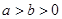 ),F
),F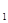 (-c,0)和F
(-c,0)和F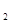 (c,0)分別是橢圓的左、右焦點,
(c,0)分別是橢圓的左、右焦點,
因此可知,當滿足延長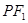 到M,使
到M,使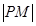 =
=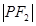 時,則點M的軌跡就是一個圓,故命題1正確
時,則點M的軌跡就是一個圓,故命題1正確
對于命題2,P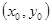 是橢圓上的動點,則
是橢圓上的動點,則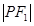
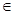
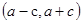 ,不符合兩點的距離公式,可以結合函數來得到端點值成立,因此為閉區間,所以錯誤。
,不符合兩點的距離公式,可以結合函數來得到端點值成立,因此為閉區間,所以錯誤。
命題3中,以焦點半徑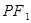 為直徑的圓必與以長軸為直徑的圓內切;這是利用了兩圓的位置關系來判定其結論,成立。
為直徑的圓必與以長軸為直徑的圓內切;這是利用了兩圓的位置關系來判定其結論,成立。
命題4中,點在橢圓上,結合導數的幾何意義表示出斜率,那么可知其切線方程為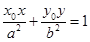 成立。
成立。
命題5中,焦點三角形的面積公式,結合定義和余弦定理可知結論為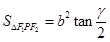 ,因此錯誤,故填寫①③④
,因此錯誤,故填寫①③④
考點:本試題考查了橢圓的方程與性質。
點評:對于橢圓中的定義和性質,以及其切線方程的求解,都可以借助于圓的思想來得到,找到切點,切線的斜率,結合點斜式方程來得到結論。屬于中檔題。


湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com