
一條直線
l被兩條直線:4x+3y+6=0和3x-5y-6=0截得的線段中心恰好是坐標原點,求直線l的方程.|
解法 1:當直線的斜率存在時由題意知,直線l過原點,則設直線l的方程為y=kx.由 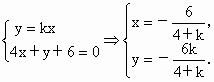
由 ∵點(0,0)是上述兩個點的中點, ∴ 解可得 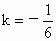 . .
∴ 所求直線的方程為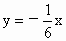 ,即為x+6y=0. ,即為x+6y=0.
當直線的斜率不存在時,直線即為 y軸,而y軸和兩條已知直線的交點分別為(0,-6)和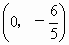 ,顯然不滿足中點為原點的要求. ,顯然不滿足中點為原點的要求.
綜上可知所求直線的方程為 x+6y=0.解法 2:依題意知l過原點,當直線的斜率存在時可設l的方程為y=kx.設 l與兩已知直線的交點分別為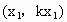 , ,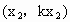 , ,
則 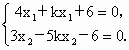 解得 解得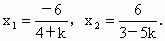
又根據中點坐標公式有  解得 解得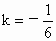 . .
因為當 k不存在時,l即為軸,而y軸和兩已知直線的交點分別為(0,6)和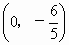 ,顯然不滿足中點是原點的要求.因此所求直線方程為 ,顯然不滿足中點是原點的要求.因此所求直線方程為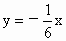 ,即x+6y=0. ,即x+6y=0.
解法 3:設所求直線l與直線4x+y+6=0,以及3x-5y-6=0的交點分別為A、B,且A(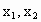 ), ),
∵ 線段AB中點為坐標原點(0,0),則點B坐標為B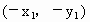 . .
又由點 A、B分別在已知直線上,∴ ∴ 又 ∵直線l過原點,∴ 直線l斜率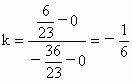 , ,
直線 l方程為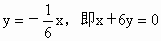 . .
|
|
方法1:由于所求直線被兩條已知直線截得線段的中點為坐標原點,即所求的直線經過坐標原點,因此所求的直線方程可以設為 方法2:由于直線 l與兩已知直線交點所得線段中點恰為坐標原點,因此,可設一個交點坐標為 |


 天天向上課時同步訓練系列答案
天天向上課時同步訓練系列答案 陽光課堂同步練習系列答案
陽光課堂同步練習系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com