
(1)求![]() 的單調區間和值域;
的單調區間和值域;
(2)設a≥1,函數g(x)=x3-3a2x-2a,x∈[0,1],若對于任意x1∈[0,1],總存在x0∈[0,1],使得g(x0)=f(x1)成立,求a的取值范圍.
解析:(1)對函數![]() 求導,得?
求導,得?
![]() =
=![]() ?
?
令![]() =0,解得x=
=0,解得x=![]() 或x=
或x=![]() .?
.?
當x變化時,f′(x)、![]() 的變化情況如下表:
的變化情況如下表:
| |||||
|
|
|
| ||
所以,當x∈(0, ![]() )時,
)時, ![]() 是減函數;當x∈(
是減函數;當x∈(![]() ,1)時,
,1)時, ![]() 是增函數.?
是增函數.?
當x∈[0,1]時, ![]()
![]() 的值域為[-4,-3].?
的值域為[-4,-3].?
(2)對函數g(x)求導,得g′(x)=3(x2-a2).?
因為a≥1,當x∈(0,1)時,g′(x)<3(1-a2)≤0,?
即當x∈(0,1)時,g(x)為減函數,從而當x∈[0,1]時有g(x)∈[g(1),g(0)].?
又g(1)=1-2a-3a2,g(0)=-2a,即當x∈[0,1]時有g(x)∈[1-2a-3a2,-2a].?
任給x1∈[0,1],f(x1)∈[-4,-3],存在x0∈[0,1]使得g(x0)=f(x1),則[1-2a-3a2,-2a][-4,-3],?
即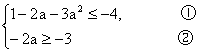 ?
?
解①式得a≥1或a≤-![]() ;?
;?
解②式得a≤![]() .?
.?
又a≥1,故a的取值范圍為1≤a≤![]() .
.


 怎樣學好牛津英語系列答案
怎樣學好牛津英語系列答案科目:高中數學 來源: 題型:
| yz |
| xz |
| xy |
查看答案和解析>>
科目:高中數學 來源: 題型:
(本小題滿分13分)已知函數![]() (x>0)在x = 1處
(x>0)在x = 1處
取得極值–3–c,其中a,b,c為常數。
(1)試確定a,b的值;
(2)討論函數f(x)的單調區間;
(3)若對任意x>0,不等式![]() 恒成立,求c的取值范圍。
恒成立,求c的取值范圍。
查看答案和解析>>
科目:高中數學 來源: 題型:
(本小題滿分12分)已知函數![]() (x>0)在x = 1處取得極值
(x>0)在x = 1處取得極值![]() ,其中a,b,c為常數。
,其中a,b,c為常數。
(1)試確定a,b的值; (2) 討論函數f(x)的單調區間;
(3)若對任意x>0,不等式![]() 恒成立,求c的取值范圍。
恒成立,求c的取值范圍。
查看答案和解析>>
科目:高中數學 來源: 題型:
已知函數![]() (x>0)在x = 1處取得極值
(x>0)在x = 1處取得極值![]() ,其中a,b,c為常數。(1)試確定a,b的值; (2)討論函數f(x)的單調區間;
,其中a,b,c為常數。(1)試確定a,b的值; (2)討論函數f(x)的單調區間;
(3)若對任意x>0,不等式![]() 恒成立,求c的取值范圍。
恒成立,求c的取值范圍。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com