
【題目】已知函數![]() (
(![]() ,且
,且![]() 、
、![]() ).設關于
).設關于![]() 的不等式
的不等式![]() 的解集為
的解集為![]() ,且方程
,且方程![]() 的兩實根為
的兩實根為![]() 、
、![]() .
.
(1)若![]() ,完成下列問題:
,完成下列問題:
①求![]() 、
、![]() 的關系式;
的關系式;
②若![]() 、
、![]() 都是負整數,求
都是負整數,求![]() 的解析式;
的解析式;
(2)若![]() ,求證:
,求證: ![]() .
.
【答案】(1)①![]() ;②
;②![]() ;(2)見解析.
;(2)見解析.
【解析】
(1)①要求![]() 、
、![]() 的關系式,可根據方程
的關系式,可根據方程![]() 的兩實根為
的兩實根為![]() 、
、![]() .結合韋達定理(根與系數的關系),用
.結合韋達定理(根與系數的關系),用![]() 、
、![]() 表示
表示![]() 、
、![]() .又則
.又則![]() ,給出
,給出![]() 、
、![]() 的關系,但在分析過程中,要注意方程有兩個不相等的根時,方程的判別式大于零;
的關系,但在分析過程中,要注意方程有兩個不相等的根時,方程的判別式大于零;
②由![]() 可得出
可得出![]() ,由題意可得出
,由題意可得出![]() ,由此得出
,由此得出![]() ,且
,且![]() ,可解出
,可解出![]() 的取值范圍,進而可求出負整數
的取值范圍,進而可求出負整數![]() 、
、![]() 的值,從而可得出函數
的值,從而可得出函數![]() 的解析式;
的解析式;
(2)由![]() ,根據零點的存在定理可以得到
,根據零點的存在定理可以得到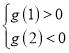 ,代入可以構造一個關于
,代入可以構造一個關于![]() 、
、![]() 的不等式組,畫出它們表示的平面區域,利用線性規劃不難得到結論.
的不等式組,畫出它們表示的平面區域,利用線性規劃不難得到結論.
(1)①由![]() ,得
,得![]() ,由已知得
,由已知得![]() ,
,
由韋達定理得![]() ,
,![]() ,
,
則![]() ,化簡得
,化簡得![]() ,
,
所以,![]() 、
、![]() 的關系式為
的關系式為![]() ;
;
②![]() ,得
,得![]() ,
,
因為![]() 、
、![]() 均為負整數,則
均為負整數,則![]() ,
,![]() 且
且![]() 、
、![]() ,
,
由![]() 可得
可得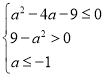 ,解得
,解得![]() .
.
![]() ,
,![]() ,當
,當![]() 時,
時,![]() (舍);當
(舍);當![]() 時,
時,![]() ,合乎題意.
,合乎題意.
綜上所述,![]() ;
;
(2)令![]() ,
,
又![]() ,
,![]() ,則
,則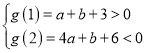 ,
,
又因為方程![]() 的兩根為
的兩根為![]() 、
、![]() ,則
,則![]() ,
,![]() ,
,
![]() ,
,
作出不等式組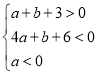 所表示的可行域如下圖所示:
所表示的可行域如下圖所示:
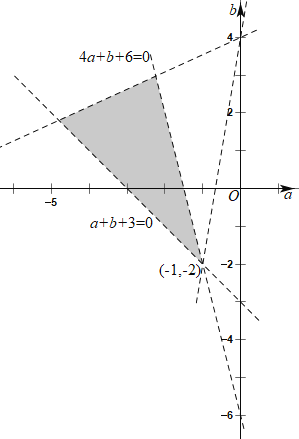
由圖象可知,![]() ,所以,
,所以,![]() ,
,
因此,![]() .
.


科目:高中數學 來源: 題型:
【題目】為了解某班學生喜愛打籃球是否與性別有關,對該班40名學生進行了問卷調查,得到了如下的![]() 列聯表:
列聯表:
男生 | 女生 | 總計 | |
喜愛打籃球 | 19 | 15 | 34 |
不喜愛打籃球 | 1 | 5 | 6 |
總計 | 20 | 20 | 40 |
(1)在女生不喜愛打籃球的5個個體中,隨機抽取2人,求女生甲被選中的概率;
(2)判斷能否在犯錯誤的概率不超過![]() 的條件下認為喜愛籃球與性別有關?
的條件下認為喜愛籃球與性別有關?
附: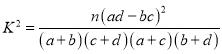 ,其中
,其中![]() .
.
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | <>0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,圓
中,圓![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),圓
為參數),圓![]() 與圓
與圓![]() 外切于原點
外切于原點![]() ,且兩圓圓心的距離
,且兩圓圓心的距離![]() ,以坐標原點為極點,
,以坐標原點為極點,![]() 軸正半軸為極軸建立極坐標系.
軸正半軸為極軸建立極坐標系.
(1)求圓![]() 和圓
和圓![]() 的極坐標方程;
的極坐標方程;
(2)過點![]() 的直線
的直線![]() ,
,![]() 與圓
與圓![]() 異于點
異于點![]() 的交點分別為點
的交點分別為點![]() ,
,![]() ,與圓
,與圓![]() 異于點
異于點![]() 的交點分別為點
的交點分別為點![]() ,
,![]() ,且
,且![]() ,求四邊形面積
,求四邊形面積![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知過橢圓![]() 的四個頂點與坐標軸垂直的四條直線圍成的矩形
的四個頂點與坐標軸垂直的四條直線圍成的矩形![]() (
(![]() 是第一象限內的點)的面積為
是第一象限內的點)的面積為![]() ,且過橢圓
,且過橢圓![]() 的右焦點
的右焦點![]() 的傾斜角為
的傾斜角為![]() 的直線過點
的直線過點![]() .
.
(1)求橢圓![]() 的標準方程
的標準方程
(2)若射線![]() 與橢圓
與橢圓![]() 的交點分別為
的交點分別為![]() .當它們的斜率之積為
.當它們的斜率之積為![]() 時,試問
時,試問![]() 的面積是否為定值?若為定值,求出此定值;若不為定值,說明理由.
的面積是否為定值?若為定值,求出此定值;若不為定值,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“干支紀年法”是中國歷法上自古以來使用的紀年方法,甲、乙、丙、丁、戊、己、庚、辛、壬、癸被稱為“十天干”,子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥叫做“十二地支”。“天干”以“甲”字開始,“地支”以“子”字開始,兩者按干支順序相配,組成了干支紀年法,其相配順序為:甲子、乙丑、丙寅…癸酉,甲戌、乙亥、丙子…癸未,甲申、乙酉、丙戌…癸巳,…,共得到60個組合,稱六十甲子,周而復始,無窮無盡。2019年是“干支紀年法”中的己亥年,那么2026年是“干支紀年法”中的
A. 甲辰年B. 乙巳年C. 丙午年D. 丁未年
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某控制器中有一個易損部件,現統計了30個該部件的使用壽命,結果如下(單位:小時);
710 721 603 615 760 742 841 591 590 721 718 750 760 713 709
681 736 654 722 732 722 715 726 699 755 751 709 733 705 700
(1)估計該部件的使用壽命達到一個月及以上的概率(一個月按30天計算);
(2)為了保證該控制器能穩定工作,將若干個同樣的部件按下圖連接在一起組成集成塊,每一個部件是否能正常工作互不影響.對比![]() 和
和![]() 時,哪個能保證集成塊使用壽命達到一個月及以上的概率超過0.8?
時,哪個能保證集成塊使用壽命達到一個月及以上的概率超過0.8?
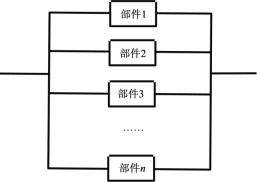
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com