
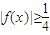 成立.
成立. ,設(shè)g(x)=|f(x)|,g(x)在x∈[-1,1]上是偶函數(shù),故只要證明當(dāng)x∈[0,1]時,
,設(shè)g(x)=|f(x)|,g(x)在x∈[-1,1]上是偶函數(shù),故只要證明當(dāng)x∈[0,1]時, ,分a小于等于0和a大于0小于
,分a小于等于0和a大于0小于 兩種情況,討論f'(x)的正負(fù)化簡絕對值并得到函數(shù)的增減區(qū)間,根據(jù)函數(shù)的增減性分別求出|f(x)|的最小值比
兩種情況,討論f'(x)的正負(fù)化簡絕對值并得到函數(shù)的增減區(qū)間,根據(jù)函數(shù)的增減性分別求出|f(x)|的最小值比 大得證.
大得證. ;
; 成立等價于當(dāng)x∈[-1,1]時,
成立等價于當(dāng)x∈[-1,1]時, ,
, ,
, ;
; ,
, ,列表:
,列表:
 上遞減,在
上遞減,在 上遞增,
上遞增, ,
, 時,g(x)=-f(x),
時,g(x)=-f(x), 時,g(x)=f(x),
時,g(x)=f(x), ,
, ,即
,即 ,則
,則
 ,即
,即 ,則
,則 ;
; 成立.
成立.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案科目:高中數(shù)學(xué) 來源: 題型:
| 1 | 4 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
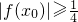 成立.
成立.查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010年遼寧省丹東市高考數(shù)學(xué)二模試卷(理科)(解析版) 題型:解答題
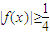 成立.
成立.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com