
【題目】已知函數![]() ,
,![]() .
.
(1)當![]() 時,若直線
時,若直線![]() 是函數
是函數![]() 的圖象的切線,求
的圖象的切線,求![]() 的最小值;
的最小值;
(2)設函數![]() ,若
,若![]() 在
在![]() 上存在極值,求
上存在極值,求![]() 的取值范圍,并判斷極值的正負.
的取值范圍,并判斷極值的正負.
【答案】(1)![]() ;(2)當
;(2)當![]() 時,
時,![]() 在
在![]() 上存在極值,且極值都為正數.
上存在極值,且極值都為正數.
【解析】
(1) 設切點坐標為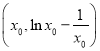 ,求得切線的方程,由直線
,求得切線的方程,由直線![]() 是函數
是函數![]() 的圖象的切線,得到
的圖象的切線,得到![]() ,
,![]() ,求得
,求得![]() ,利用導數即可求得
,利用導數即可求得![]() 的最小值.
的最小值.
(2)![]() 求出
求出![]() 的導數
的導數![]() ,令
,令![]() ,若
,若![]() 在
在![]() 上存在極值,則
上存在極值,則![]() 或
或 ,分類討論,分別構造新函數,根據導數與函數的關系,即可求得
,分類討論,分別構造新函數,根據導數與函數的關系,即可求得![]() 的取值范圍.
的取值范圍.
(1)設切點坐標為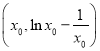 ,
,
![]() ,
,
切線斜率![]() ,又
,又![]() ,
,
![]() ,
,![]()
令![]() ,
,
![]() ,
,
解![]() 得
得![]() ,解
,解![]() 得
得![]() ,
,![]() 在
在![]() 上遞減,在
上遞減,在![]() 上遞增.
上遞增.
![]() ,
,![]() 的最小值為
的最小值為![]() .
.
(2)![]() ,
,![]() .
.
![]() .
.
設![]() ,則
,則![]() .
.
由![]() ,得
,得![]() .
.
當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]() .
.
![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減.
上單調遞減.
且![]() ,
,![]() ,
,![]() .
.
顯然![]() .
.
結合函數圖象可知,若![]() 在
在![]() 上存在極值,
上存在極值,
則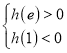 或
或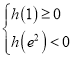
(ⅰ)當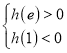 ,即
,即![]() 時,
時,
則必定![]() ,
,![]() ,使得
,使得![]() ,且
,且![]() .
.
當![]() 變化時,
變化時,![]() ,
,![]() ,
,![]() 的變化情況如下表:
的變化情況如下表:
|
|
|
|
|
|
| - | 0 | + | 0 | - |
| - | 0 | + | 0 | - |
| ↘ | 極小值 | ↗ | 極大值 | ↘ |
∴當![]() 時,
時,![]() 在
在![]() 上的極值為
上的極值為![]() ,
,![]() ,且
,且![]() .
.
![]() .
.
設![]() ,其中
,其中![]() ,
,![]() .
.
![]() ,
,![]() 在
在![]() 上單調遞增,
上單調遞增,![]() ,當且僅當
,當且僅當![]() 時取等號.
時取等號.
![]() ,
,![]() .
.
∴當![]() 時,
時,![]() 在
在![]() 上的極值
上的極值![]() .
.
(ⅱ)當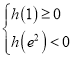 ,即
,即![]() 時,
時,
則必定![]() ,使得
,使得![]() .
.
易知![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減.
上單調遞減.
此時,![]() 在
在![]() 上的極大值是
上的極大值是![]() ,且
,且![]() .
.
∴當![]() 時,
時,![]() 在
在![]() 上的極值為正數.
上的極值為正數.
綜上所述:當![]() 時,
時,![]() 在
在![]() 上存在極值,且極值都為正數.
上存在極值,且極值都為正數.
注:也可由![]() ,得
,得![]() .令
.令![]() 后再研究
后再研究![]() 在
在![]() 上的極值問題.若只求
上的極值問題.若只求![]() 的范圍.
的范圍.


 英才計劃同步課時高效訓練系列答案
英才計劃同步課時高效訓練系列答案科目:高中數學 來源: 題型:
【題目】設等差數列{an}的前n項和為Sn,若S9=81,a3+a5=14.
(1)求數列{an}的通項公式;
(2)設bn=![]() ,若{bn}的前n項和為Tn,證明:Tn<
,若{bn}的前n項和為Tn,證明:Tn<![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】關于函數![]() 有下述四個結論:
有下述四個結論:
①![]() 是偶函數;②
是偶函數;②![]() 的最大值為
的最大值為![]() ;
;
③![]() 在
在![]() 有
有![]() 個零點;④
個零點;④![]() 在區間
在區間![]() 單調遞增.
單調遞增.
其中所有正確結論的編號是( )
A.①②B.①③C.②④D.①④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】
在平面直角坐標系xOy中,曲線C的參數方程為![]() (a為參數),在以原點為極點,x軸正半軸為極軸的極坐標系中,直線l的極坐標方程為
(a為參數),在以原點為極點,x軸正半軸為極軸的極坐標系中,直線l的極坐標方程為![]() .
.
(1)求C的普通方程和l的傾斜角;
(2)設點![]() ,l和C交于A,B兩點,求
,l和C交于A,B兩點,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某汽車美容公司為吸引顧客,推出優惠活動:對首次消費的顧客,按![]() /次收費,并注冊成為會員,對會員逐次消費給予相應優惠,標準如下:
/次收費,并注冊成為會員,對會員逐次消費給予相應優惠,標準如下:
消費次第 | 第 | 第 | 第 | 第 |
|
收費比率 |
|
|
|
|
|
該公司注冊的會員中沒有消費超過![]() 次的,從注冊的會員中,隨機抽取了100位進行統計,得到統計數據如下:
次的,從注冊的會員中,隨機抽取了100位進行統計,得到統計數據如下:
消費次數 |
|
|
|
|
|
人數 |
|
|
|
|
|
假設汽車美容一次,公司成本為![]() 元,根據所給數據,解答下列問題:
元,根據所給數據,解答下列問題:
(1)某會員僅消費兩次,求這兩次消費中,公司獲得的平均利潤;
(2)以事件發生的頻率作為相應事件發生的概率,設該公司為一位會員服務的平均利潤為![]() 元,求
元,求![]() 的分布列和數學期望
的分布列和數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面ABCD為梯形,AB//CD,
中,底面ABCD為梯形,AB//CD,![]() ,AB=AD=2CD=2,△ADP為等邊三角形.
,AB=AD=2CD=2,△ADP為等邊三角形.
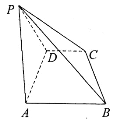
(1)當PB長為多少時,平面![]() 平面ABCD?并說明理由;
平面ABCD?并說明理由;
(2)若二面角![]() 大小為150°,求直線AB與平面PBC所成角的正弦值.
大小為150°,求直線AB與平面PBC所成角的正弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com