
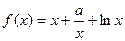 ,
,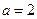 時,求函數(shù)
時,求函數(shù) 的單調增區(qū)間;
的單調增區(qū)間; 是否存在極值.
是否存在極值. 的定義域為
的定義域為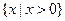 ………………2分
………………2分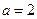 時,
時,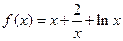 ,
,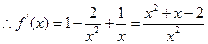 ……3分
……3分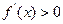 ,即
,即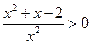 ,得
,得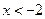 或
或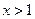 ………………5分
………………5分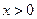 ,所以,函數(shù)
,所以,函數(shù) 的單調增區(qū)間為
的單調增區(qū)間為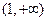 ………………6分
………………6分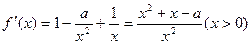 ……………7分
……………7分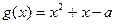 ,因為
,因為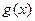 對稱軸
對稱軸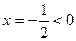 ,所以只需考慮
,所以只需考慮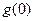 的正負,
的正負,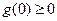 即
即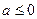 時,在(0,+∞)上
時,在(0,+∞)上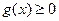 ,
, 在(0,+∞)單調遞增,
在(0,+∞)單調遞增, 無極值 ………………10分
無極值 ………………10分 即
即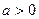 時,
時,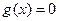 在(0,+∞)有解,所以函數(shù)
在(0,+∞)有解,所以函數(shù) 存在極值.…
存在極值.… 12分
12分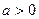 時,函數(shù)
時,函數(shù) 存在極值;當
存在極值;當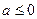 時,函數(shù)
時,函數(shù) 不存在極值.…14分
不存在極值.…14分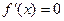 即
即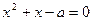 ,記
,記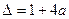
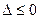 即
即
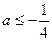 時,
時,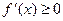 ,
, 在(0,+∞)單調遞增,無極值 ………9分
在(0,+∞)單調遞增,無極值 ………9分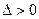 即
即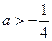 時,解
時,解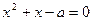 得:
得: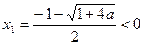 或
或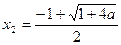
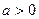 則
則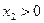 ,列表如下:
,列表如下: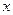 | (0, ) ) |  | ( ,+∞) ,+∞) |
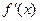 | — | 0 | + |
 | ↘ | 極小值 | ↗ |
 時函數(shù)
時函數(shù) 取到極小值,即
取到極小值,即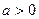 函數(shù)
函數(shù) 存在極小值。………11分
存在極小值。………11分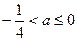 ,則
,則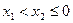 ,
, 在(0,+∞)單調遞減,不存在極值。……13分
在(0,+∞)單調遞減,不存在極值。……13分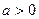 時,函數(shù)
時,函數(shù) 存在極值,當
存在極值,當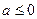 時。函數(shù)
時。函數(shù) 不存在極值……14分
不存在極值……14分

 芝麻開花課程新體驗系列答案
芝麻開花課程新體驗系列答案科目:高中數(shù)學 來源:不詳 題型:解答題
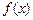 =
=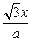 +
+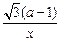 ,a≠0且a≠1.
,a≠0且a≠1.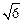 )上單調遞減,在(
)上單調遞減,在(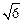 ,
,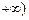 上單調遞增,求a的值并寫出函數(shù)的解析式;
上單調遞增,求a的值并寫出函數(shù)的解析式;查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
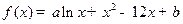 的一個極值點,(
的一個極值點,(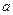 ,b∈R).
,b∈R).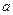 的值;
的值; 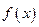 的單調區(qū)間;
的單調區(qū)間;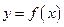 有3個不同的零點,求
有3個不同的零點,求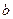 的取值范圍.
的取值范圍.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
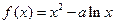 (常數(shù)
(常數(shù)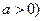 .
.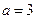 時,求曲線
時,求曲線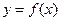 在點
在點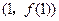 處的切線方程;
處的切線方程;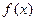 在區(qū)間
在區(qū)間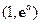 上零點的個數(shù)(
上零點的個數(shù)(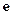 為自然對數(shù)的底數(shù)).
為自然對數(shù)的底數(shù)).查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com