【題目】如圖，在邊長為2的正方體ABCD-A1B1C1D1中，E是BC的中點，F是DD1的中點，
（1）求證：CF∥平面A1DE；
（2）求平面A1DE與平面A1DA夾角的余弦值．
【答案】（1）見解析；（2）
【解析】
（1）以D為原點，分別以DA，DC，DD1為x軸，y軸，z軸建立空間直角坐標系，利用向量法能證明CF∥平面A1DE．
（2）求出平面A1DE的法向量和平面A1DA的法向量，利用向量法能求出平面A1DE與平面A1DA夾角的余弦值．
證明：（1）以D為原點，分別以DA，DC，DD1為x軸，y軸，z軸建立空間直角坐標系，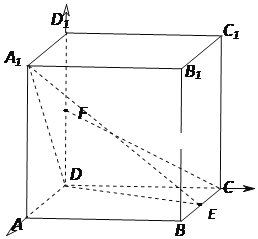
則A（2，0，0），A1（2，0，2），E（1，2，0），D（0，0，0），B1（2，2，2），
則
，
設平面A1DE的法向量是
則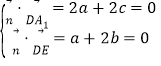
，取
，
∴
所以CF∥平面A1DE．
解：（2）
是面A1DA的法向量，
∴
即平面A1DE與平面A1DA夾角的余弦值為．
開心蛙狀元測試卷系列答案科目：高中數學 來源： 題型：
【題目】一家面包房根據以往某種面包的銷售記錄，繪制了日銷售量的頻率分布直方圖，如圖231所示．
圖231
將日銷售量落入各組的頻率視為概率，并假設每天的銷售量相互獨立．
(1)求在未來連續3天里，有連續2天的日銷售量都不低于100個且另1天的日銷售量低于50個的概率；
(2)用X表示在未來3天里日銷售量不低于100個的天數，求隨機變量X的分布列，期望E(X)及方差D(X)．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了測量某塔的高度，某人在一條水平公路
兩點進行測量.在
點測得塔底
在南偏西
，塔頂仰角為
，此人沿著南偏東
方向前進10米到
點，測得塔頂的仰角為
，則塔的高度為（ ）
A. 5米B. 10米C. 15米D. 20米
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知平面向量
，
滿足：||＝2，||＝1．
（1）若（
2）（
）＝1，求的值；
（2）設向量，的夾角為θ．若存在t∈R，使得
，求cosθ的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】四棱錐
中,底面
是邊長為
的菱形,側面
底面
,
60°, 
, 
是
中點,點
在側棱
上.
（Ⅰ）求證: 
;
（Ⅱ）是否存在
,使平面
平面
？若存在,求出,若不存在,說明理由.
（Ⅲ）是否存在
,使
平面
？若存在,求出.若不存在,說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某校為了解甲、乙兩班學生的學業水平,從兩班中各隨機抽取
人參加學業水平等級考試,得到學生的學業成績莖葉圖如圖:
（Ⅰ）通過莖葉圖比較甲、乙兩班學生的學業成績平均值
與
及方差
與
的大小;（只需寫出結論）
（Ⅱ）根據學生的學業成績,將學業水平分為三個等級:
根據所給數據,頻率可以視為相應的概率.
（i）從甲、乙兩班中各隨機抽取
人,記事件
:“抽到的甲班學生的學業水平高于乙班學生的學業水平等級”,求
發生的概率;
（ii）從甲班中隨機抽取
人,記
為學業水平優秀的人數,求
的分布列和數學期望.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某地區某農產品近幾年的產量統計如表：
（1）根據表中數據，建立
關于
的線性回歸方程
；
（2）根據線性回歸方程預測2019年該地區該農產品的年產量.
附:對于一組數據
，其回歸直線的斜率和截距的最小二乘估計分別為：
，
.(參考數據: 
，計算結果保留小數點后兩位）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】按規定：車輛駕駛員血液酒精濃度在20—80mg/100ml（不含80）之間，屬酒后駕車；在
（含80）以上時，屬醉酒駕車．某市交警在某路段的一次攔查行動中，依法檢查了250輛機動車，查出酒后駕車和醉酒駕車的駕駛員20人，右圖是對這20人血液中酒精含量進行檢查所得結果的頻率分布直方圖．
（1）根據頻率分布直方圖，求：此次抽查的250人中，醉酒駕車的人數；
（2）從血液酒精濃度在
范圍內的駕駛員中任取2人，求恰有1人屬于醉酒駕車的概率．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
