【題目】已知定義域為
的函數
是奇函數.
（1）求
，判斷函數
的單調性并證明.
（2）對任意的
，不等式
恒成立，求
的取值范圍.
鴻圖圖書寒假作業假期作業吉林大學出版社系列答案科目：高中數學 來源： 題型：
【題目】如圖，在邊長為2的正方體ABCD-A1B1C1D1中，E是BC的中點，F是DD1的中點，
（1）求證：CF∥平面A1DE；
（2）求平面A1DE與平面A1DA夾角的余弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列事件是隨機事件的是（ ）
①當x>10時，
； ②當x∈R，x2+x＝0有解
③當a∈R關于x的方程x2+a＝0在實數集內有解； ④當sinα>sinβ時，α>β（ ）
A.①②B.②③C.③④D.①④
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示，某區有一塊空地
，其中
，
，
.當地區政府規劃將這塊空地改造成一個旅游景點，擬在中間挖一個人工湖
，其中
都在邊
上，且
，挖出的泥土堆放在
地帶上形成假山，剩下的
地帶開設兒童游樂場.為安全起見，需在
的周圍安裝防護網.
（1）當
時，求防護網的總長度；
（2）若要求挖人工湖用地的面積是堆假山用地的面積的
倍，試確定
的大小；
（3）為節省投入資金，人工湖的面積要盡可能小，問如何設計施工方案，可使的面積最小？最小面積是多少？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知平面上一個圓可以將平面分成兩個部分，兩個圓最多可以將平面分成4個部分，設平面上
個圓最多可以將平面分成
個部分．
求
，
的值；
猜想的表達式并證明；
證明：
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（本小題共13分）
已知
， 
或1， 
，對于
， 
表示U和V中相對應的元素不同的個數．
（Ⅰ）令
，存在m個
，使得
，寫出m的值；
（Ⅱ）令
，若
，求證： 
；
（Ⅲ）令
，若
，求所有
之和．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知直線
， (
為參數， 
為傾斜角).以坐標原點為極點， 
軸的正半軸為極軸建立極坐標系，曲線
的直角坐標方程為
.
（Ⅰ）將曲線
的直角坐標方程化為極坐標方程；
（Ⅱ）設點
的直角坐標為
，直線
與曲線
的交點為
、
，求
的取值范圍.
【答案】（I）
；（II）
.
【解析】試題分析：（Ⅰ）將由
代入
，化簡即可得到曲線
的極坐標方程；（Ⅱ）將
的參數方程
代入
，得
，根據直線參數方程的幾何意義，利用韋達定理結合輔助角公式，由三角函數的有界性可得結果.
試題解析：（Ⅰ）由
及
，得
，即
所以曲線
的極坐標方程為
（II）將
的參數方程
代入
，得
∴
, 所以
，又
，
所以
，且
,
所以
,
由
，得
，所以
.
故
的取值范圍是
.
【題型】解答題
【結束】
23
【題目】已知
、
、
均為正實數.
（Ⅰ）若
，求證： 
（Ⅱ）若
，求證： 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某學校高三年級學生某次身體素質體能測試的原始成績采用百分制，已知所有這些學生的原始成績均分布在
內，發布成績使用等級制，各等級劃分標準見下表．
百分制 | 85分及以上 | 70分到84分 | 60分到69分 | 60分以下 |
等級 | A | B | C | D |
規定：A，B，C三級為合格等級，D為不合格等級為了解該校高三年級學生身體素質情況，從中抽取了n名學生的原始成績作為樣本進行統計．
按照
，
，
，
，
的分組作出頻率分布直方圖如圖1所示，樣本中分數在80分及以上的所有數據的莖葉圖如圖2所示
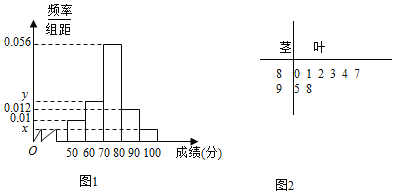
求n和頻率分布直方圖中的x，y的值，并估計該校高一年級學生成績是合格等級的概率；
根據頻率分布直方圖，求成績的中位數
精確到
；
在選取的樣本中，從A，D兩個等級的學生中隨機抽取2名學生進行調研，求至少有一名學生是A等級的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】省環保廳對
、
、
三個城市同時進行了多天的空氣質量監測，測得三個城市空氣質量為優或良的數據共有180個，三城市各自空氣質量為優或良的數據個數如下表所示：
|
|
| |
優（個） | 28 |
|
|
良（個） | 32 | 30 |
|
已知在這180個數據中隨機抽取一個，恰好抽到記錄
城市空氣質量為優的數據的概率為0.2.
（1）現按城市用分層抽樣的方法，從上述180個數據中抽取30個進行后續分析，求在
城中應抽取的數據的個數；
（2）已知
， 
，求在
城中空氣質量為優的天數大于空氣質量為良的天數的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
