
【題目】已知函數![]() ,其中
,其中![]() .
.
(1)若x=2是函數f(x)的極值點,求![]() 在(1,h(1))處的切線方程;
在(1,h(1))處的切線方程;
(2)若對任意的![]() (
(![]() 為自然對數的底數)都有
為自然對數的底數)都有![]() 成立,求實數
成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
試題分析:(1)由![]() 是極值點,可知
是極值點,可知![]() ,從而可得
,從而可得![]() 值,再求出
值,再求出![]() ,得
,得![]() ,此為切線斜率,切線方程為
,此為切線斜率,切線方程為![]() ,化簡即可;(2)對本小題命題,可求出
,化簡即可;(2)對本小題命題,可求出![]() 的最小值
的最小值![]() 和
和![]() 的最大值
的最大值![]() ,命題可轉化為
,命題可轉化為![]() ,然后可求得
,然后可求得![]() 的范圍,
的范圍,![]() 最大值由導數的性質易求,由于
最大值由導數的性質易求,由于![]() 中含有參數
中含有參數![]() ,求其最小值時要分類討論.
,求其最小值時要分類討論.
試題解析:(1)解:∵![]() , ∵x=2是函數f(x)的極值點,
, ∵x=2是函數f(x)的極值點,
∴![]() , 即
, 即![]() .又a≥1, ∴a=2
.又a≥1, ∴a=2
∴![]() , ∴
, ∴![]() ,
,
∴![]() , 又h(1)=6
, 又h(1)=6
∴所求的切線方程是 y-1=-(x-6),即 y=-x+7.
(2)解:對任意的![]() 都有
都有![]() ≥
≥![]() 成立等價于對任意的
成立等價于對任意的![]() 都有
都有![]() ≥
≥![]()
當![]()
![]() [1,
[1,![]() ]時,
]時,![]() .
.
∴函數![]() 在
在![]() 上是增函數.
上是增函數.
∴![]() .
.
∵![]() ,且
,且![]() ,
,![]() .
.
① 當1≤![]() ≤
≤![]() 時,
時,
若1≤![]() <
<![]() ,則
,則![]() ,
,
若![]() <
<![]() ≤
≤![]() ,則
,則![]() .
.
∴函數![]() 在
在![]() 上是減函數,在
上是減函數,在![]() 上是增函數.
上是增函數.
∴![]() .
.
由![]() ≥
≥![]() ,得
,得![]() ≥
≥![]() , 又1≤
, 又1≤![]() ≤
≤![]() ,∴
,∴![]() ≤
≤![]() ≤
≤![]() .
.
②.當![]() 且
且![]()
![]() [1,
[1,![]() ]時,
]時,![]() ,
,
∴函數![]() 在
在![]() 上是減函數.
上是減函數.
∴![]() .由
.由![]() ≥
≥![]() ,得
,得![]() ≥
≥![]() ,
,
又![]() ,∴
,∴![]() .
.
綜上所述,![]() 的取值范圍為
的取值范圍為![]()


 教材全解字詞句篇系列答案
教材全解字詞句篇系列答案科目:高中數學 來源: 題型:
【題目】對于定義域為D的函數![]() ,如果存在區間
,如果存在區間![]() ,同時滿足:①
,同時滿足:①![]() 在
在![]() 內是單調函數;②當定義域是
內是單調函數;②當定義域是![]() 時,
時,![]() 的值域也是
的值域也是![]() .則稱
.則稱![]() 是該函數的“和諧區間”.
是該函數的“和諧區間”.
(1)證明:![]() 是函數
是函數![]() =
=![]() 的一個“和諧區間”.
的一個“和諧區間”.
(2)求證:函數![]() 不存在“和諧區間”.
不存在“和諧區間”.
(3)已知:函數![]() (
(![]() R,
R,![]() )有“和諧區間”
)有“和諧區間” ![]() ,當
,當![]() 變化時,求出
變化時,求出![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某同學的父親決定今年夏天賣西瓜賺錢,根據去年6月份的數據統計連續五天內每天所賣西瓜的個數與溫度之間的關系如下表:
溫度 | 32 | 33 | 35 | 37 | 38 |
西瓜個數 | 20 | 22 | 24 | 30 | 34 |
(1)求這五天內所賣西瓜個數的平均值和方差;
(2)求變量![]() 之間的線性回歸方程,并預測當溫度為
之間的線性回歸方程,并預測當溫度為![]() 時所賣西瓜的個數.
時所賣西瓜的個數.
附: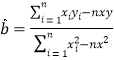 ,
,![]() (精確到
(精確到![]() ).
).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-1:幾何證明選講
如圖所示,已知PA與⊙O相切,A為切點,PBC為割線,弦CD∥AP,AD、BC相交于E點,F為CE上一點,且DE2=EF·EC.

(1)求證:P=EDF;
(2)求證:CE·EB=EF·EP.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)=ax-![]() -5ln x,g(x)=x2-mx+4.
-5ln x,g(x)=x2-mx+4.
(1)若x=2是函數f(x)的極值點,求a的值;
(2)當a=2時,若x1∈(0,1),x2∈[1,2],都有f(x1)≥g(x2)成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】四名同學根據各自的樣本數據研究變量x,y之間的相關關系,并求得回歸直線方程,分別得到以下四個結論:
①y與x負相關且![]() =2.347x-6.423;
=2.347x-6.423;
②y與x負相關且![]() =-3.476x+5.648;
=-3.476x+5.648;
③y與x正相關且![]() =5.437x+8.493;
=5.437x+8.493;
④y與x正相關且![]() =-4.326x-4.578.
=-4.326x-4.578.
其中一定不正確的結論的序號是( )
A.①② B.②③ C.③④ D.①④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市電視臺為了宣傳,舉辦問答活動,隨機對該市15至65歲的人群進行抽樣,頻率分布直方圖及回答問題統計結果如表所示:
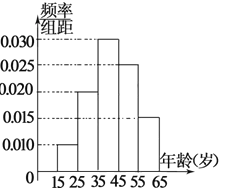
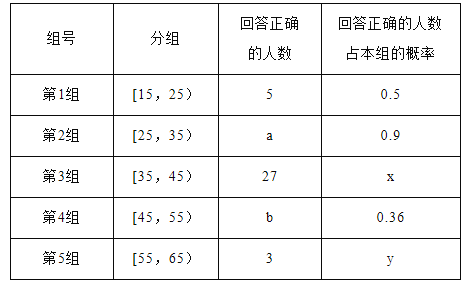
(1)分別求出![]() 的值;
的值;
(2)從第2,3,4組回答正確的人中用分層抽樣的方法抽取6人,則第2,3,4組每組應各抽取多少人?
(3)在(2)的前提下,電視臺決定在所抽取的6人中隨機抽取3人頒發幸運獎,求:所抽取的人中第3組至少有1人獲得幸運獎的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,邊長為5的正方形![]() 與矩形
與矩形![]() 所在平面互相垂直,
所在平面互相垂直,![]() 分別為
分別為![]() 的中點,
的中點,![]() .
.
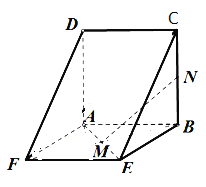
(1)求證:![]() 平面
平面![]() ;
;
(2)求證:![]() 平面
平面![]() ;
;
(3)在線段![]() 上是否存在一點
上是否存在一點![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的長;若不存在,請說明理由.
的長;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com