
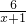 ≥1},B={x|x2-2x+2m<0}.
≥1},B={x|x2-2x+2m<0}. .…(6分)
.…(6分)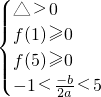 ,即
,即 ,解得-
,解得- ≤m≤
≤m≤ .…(10分)
.…(10分) .…(12分)
.…(12分)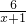 ≥1,可以求出集合A,由A∩B={x|-1<x<4},結合不等式解集的端點與方程根的關系,可得x=4必為方程x2-2x+2m=0的一根,代入構造關于m的方程,即可求出實數m的值;
≥1,可以求出集合A,由A∩B={x|-1<x<4},結合不等式解集的端點與方程根的關系,可得x=4必為方程x2-2x+2m=0的一根,代入構造關于m的方程,即可求出實數m的值; ≤m≤
≤m≤ .
. 

 閱讀快車系列答案
閱讀快車系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com