
【題目】某學校高一 、高二 、高三三個年級共有 ![]() 名教師,為調查他們的備課時間情況,通過分層
名教師,為調查他們的備課時間情況,通過分層
抽樣獲得了![]() 名教師一周的備課時間 ,數據如下表(單位 :小時):
名教師一周的備課時間 ,數據如下表(單位 :小時):
高一年級 |
|
|
|
|
| |||
高二年級 |
|
|
|
|
|
|
| |
高三年級 |
|
|
|
|
|
|
|
|
(1)試估計該校高三年級的教師人數 ;
(2)從高一年級和高二年級抽出的教師中,各隨機選取一人,高一年級選出的人記為甲 ,高二年級選出的人記為乙 ,求該周甲的備課時間不比乙的備課時間長的概率 ;
(3)再從高一、高二、高三三個年級中各隨機抽取一名教師,他們該周的備課時間分別是![]() (單位: 小時),這三個數據與表格中的數據構成的新樣本的平均數記為
(單位: 小時),這三個數據與表格中的數據構成的新樣本的平均數記為![]() ,表格中的數據平均數記為
,表格中的數據平均數記為![]() ,試判斷
,試判斷![]() 與
與![]() 的大小. (結論不要求證明)
的大小. (結論不要求證明)
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】試題分析:(1)直接根據分層抽樣方法,可得高三年級的教師共有![]() (人);(2)根據互斥事件、獨立事件的概率公式求解;(3)分別求出三組總平均值
(人);(2)根據互斥事件、獨立事件的概率公式求解;(3)分別求出三組總平均值![]() ,以及新加入的三個數
,以及新加入的三個數![]() 的平均數為9,比較大小即可.
的平均數為9,比較大小即可.
試題解析:(1)抽出的20位教師中,來自高三年級的有8名,
根據分層抽樣方法,高三年級的教師共有![]() (人)
(人)
(2)設事件為![]() “甲是現有樣本中高一年級中的第
“甲是現有樣本中高一年級中的第![]() 個教師”,
個教師”, ![]() ,
,
事件![]() “乙是現有樣本中高二年級中的第
“乙是現有樣本中高二年級中的第![]() 個教師”,
個教師”, ![]() ,
,
由題意知: ![]() ,
, ![]() ,
,
![]()
設事件![]() 為“該周甲的備課時間比乙的備課時間長”,由題意知,
為“該周甲的備課時間比乙的備課時間長”,由題意知,
![]()
所以![]()
![]()
故![]() ;
;
(3)![]() ,
, ![]() ,
,
![]()
三組總平均值![]() ,
,
新加入的三個數![]() 的平均數為9,比
的平均數為9,比![]() 小,
小,
故拉低了平均值,∴![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】如圖,已知四棱錐S﹣ABCD,底面ABCD為菱形,SA⊥平面ABCD,∠ADC=60°,E,F分別是SC,BC的中點. 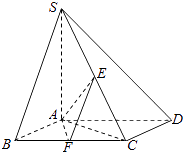
(1)證明:SD⊥AF;
(2)若AB=2,SA=4,求二面角F﹣AE﹣C的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法正確的是(只填正確說法序號)
①若集合A={y|y=x﹣1},B={y|y=x2﹣1},則A∩B={(0,﹣1),(1,0)};
② ![]() 是函數解析式;
是函數解析式;
③ ![]() 是非奇非偶函數;
是非奇非偶函數;
④設二次函數f(x)=ax2+bx+c(a≠0),若f(x1)=f(x2)(x1≠x2),則f(x1+x2)=c.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() (
(![]() )的左焦點
)的左焦點![]() 與拋物線
與拋物線![]() 的焦點重合,直線
的焦點重合,直線![]() 與以原點
與以原點![]() 為圓心,以橢圓的離心率
為圓心,以橢圓的離心率![]() 為半徑的圓相切.
為半徑的圓相切.
(Ⅰ)求該橢圓![]() 的方程;
的方程;
(Ⅱ)過點![]() 的直線交橢圓于
的直線交橢圓于![]() ,
, ![]() 兩點,線段
兩點,線段![]() 的中點為
的中點為![]() ,
, ![]() 的垂直平分線與
的垂直平分線與![]() 軸和
軸和![]() 軸分別交于
軸分別交于![]() ,
, ![]() 兩點.記
兩點.記![]() 的面積為
的面積為![]() ,
, ![]() 的面積為
的面積為![]() .問:是否存在直線
.問:是否存在直線![]() ,使得
,使得![]() ,若存在,求直線
,若存在,求直線![]() 的方程,若不存在,說明理由.
的方程,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義域為R的函數f(x)既是奇函數,又是周期為3的周期函數,當x∈(0, ![]() )時,f(x)=sinπx,f(
)時,f(x)=sinπx,f( ![]() )=0,則函數f(x)在區間[0,6]上的零點個數是( )
)=0,則函數f(x)在區間[0,6]上的零點個數是( )
A.9
B.7
C.5
D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設命題p:f(x)= ![]() 在區間(1,+∞)上是減函數;命題q;x1x2是方程x2﹣ax﹣2=0的兩個實根,不等式m2+5m﹣3≥|x1﹣x2|對任意實數α∈[﹣1,1]恒成立;若¬p∧q為真,試求實數m的取值范圍.
在區間(1,+∞)上是減函數;命題q;x1x2是方程x2﹣ax﹣2=0的兩個實根,不等式m2+5m﹣3≥|x1﹣x2|對任意實數α∈[﹣1,1]恒成立;若¬p∧q為真,試求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現有![]() (n≥2,n∈N*)個給定的不同的數隨機排成一個下圖所示的三角形數陣:
(n≥2,n∈N*)個給定的不同的數隨機排成一個下圖所示的三角形數陣:

設Mk是第k行中的最大數,其中1≤k≤n,k∈N*.記M1<M2<…<Mn的概率為pn.
(1)求p2的值;
(2)證明:pn>![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com