
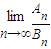 的值.
的值.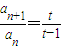 ,又ta1-1=a1,得
,又ta1-1=a1,得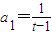 ,故數列{an}是一個以
,故數列{an}是一個以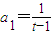 為首項,以
為首項,以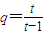 為公比的等比數列.(4分)
為公比的等比數列.(4分)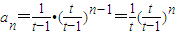 n∈N*; (6分)
n∈N*; (6分)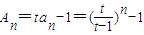 ,(7分)
,(7分)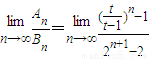 ,
,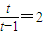 ,即t=2時,
,即t=2時,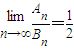 ,
,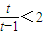 ,即t>2時,
,即t>2時,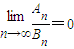 ,
,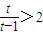 ,即1<t<2時,
,即1<t<2時,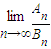 不存在.(14分)
不存在.(14分)

 新課標階梯閱讀訓練系列答案
新課標階梯閱讀訓練系列答案 口算心算速算應用題系列答案
口算心算速算應用題系列答案科目:高中數學 來源: 題型:
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com