
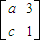
 ,矩陣A屬于特征值λ1=-1的一個特征向量為α1=
,矩陣A屬于特征值λ1=-1的一個特征向量為α1= .
. ,求A4m.
,求A4m. 1=λ
1=λ 1(
1( 1為特征向量,λ為特征值),利用矩陣的乘法法則化簡求出a與c的值,代入矩陣A即可得A,再根據矩陣A的特征多項式解出矩陣A的另一個特征值及其對應的一個特征向量;
1為特征向量,λ為特征值),利用矩陣的乘法法則化簡求出a與c的值,代入矩陣A即可得A,再根據矩陣A的特征多項式解出矩陣A的另一個特征值及其對應的一個特征向量; ,利用矩陣的乘法法則求出
,利用矩陣的乘法法則求出 =-10α1+3α2②,代入A4
=-10α1+3α2②,代入A4 中求出值即可.
中求出值即可.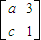
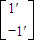 =-
=- ,即a-3=-1,c-1=1,解得a=2,b=2,
,即a-3=-1,c-1=1,解得a=2,b=2, ;
; =λ2-3λ-4=0,
=λ2-3λ-4=0, ,
,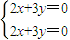 ⇒2x+3y=0.
⇒2x+3y=0. 為屬于特征值λ2=4的一個特征向量.(8分)
為屬于特征值λ2=4的一個特征向量.(8分) =pα1+qα2=p
=pα1+qα2=p +q
+q =
= ,
, 解得
解得  ,則
,則 =-10α1+3α2
=-10α1+3α2 =A4(-10α1+3α2)=-10(A4α1)+3A4α2
=A4(-10α1+3α2)=-10(A4α1)+3A4α2 α1)+3
α1)+3 α2=-10×1×
α2=-10×1× +3×256×
+3×256× =
= .
.

 智慧小復習系列答案
智慧小復習系列答案科目:高中數學 來源: 題型:
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
 附加題:(選做題:在下面A、B、C、D四個小題中只能選做兩題)
附加題:(選做題:在下面A、B、C、D四個小題中只能選做兩題)| 5 |
|
|
|
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com