
分析 (Ⅰ)求出函數的導數,問題轉化為a≥${({{\frac{1}{2}x}_{0}}^{2}{+x}_{0})}_{max}$,x0∈(0,2],根據二次函數的性質求出a的范圍即可;
(Ⅱ)求出函數f(x) 的導數,令g(x)=x2+x-a,(x≥1),通過討論a的范圍,求出函數的單調區間,結合函數的單調性求出a的范圍即可.
解答 解:(Ⅰ)依題意,知f(x)的定義域為(0,+∞),
f′(x)=$\frac{1}{x}$-$\frac{a}{{x}^{2}}$+1,x∈(0,2],
則有k=f′(x0)=$\frac{{{x}_{0}}^{2}{+x}_{0}-a}{{{x}_{0}}^{2}}$≤$\frac{1}{2}$,在x0∈(0,2]上恒成立,
所以a≥${({{\frac{1}{2}x}_{0}}^{2}{+x}_{0})}_{max}$,x0∈(0,2],
當x0=2時,$\frac{1}{2}$${{x}_{0}}^{2}$+x0取得最大值4,所以a≥4;
(Ⅱ)由不等式f(x)≥a+1,對x∈[1,+∞)恒成立,
f′(x)=$\frac{{x}^{2}+x-a}{{x}^{2}}$,令g(x)=x2+x-a,(x≥1),
則g(x)是x∈[1,+∞)上的增函數,即g(x)≥2-a,
①當a≤2時,g(x)≥0,所以f′(x)≥0,因此f(x)是x∈[1,+∞)上的增函數,
則f(x)≥f(1)=0,因此a≤2時,不等式成立;
②當a>2時,即對x∈[1,+∞),f′(x)=0時,g(x)=0,
求得x1=$\frac{-1+\sqrt{1+4a}}{2}$,(由于x≥1,所以舍去x2=-1-$\frac{-1-\sqrt{1+4a}}{2}$)
當x∈[1,$\frac{-1+\sqrt{1+4a}}{2}$)時,f′(x)<0,則f(x)是x∈[1,$\frac{-1+\sqrt{1+4a}}{2}$)上的減函數,
當x∈$\frac{-1+\sqrt{1+4a}}{2}$,+∞)時,f′(x)>0,
則f(x)是x∈($\frac{-1+\sqrt{1+4a}}{2}$,+∞)上的增函數,
所以當x∈(1,$\frac{-1+\sqrt{1+4a}}{2}$)時,f(x)<f(1)=0,
因此a>2時,不等式不成立;
綜合上述,所求范圍是a≤2.
點評 本題考查了函數的單調性問題,考查導數的應用以及函數恒成立問題,是一道中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 實驗操作 | |||||
| 不合格 | 合格 | 良好 | 優秀 | ||
| 體 能 測 試 | 不合格 | 0 | 0 | 1 | 1 |
| 合格 | 0 | 2 | 1 | b | |
| 良好 | 1 | a | 2 | 4 | |
| 優秀 | 1 | 2 | 3 | 6 | |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
 如圖,某幾何體的三視圖中,正視圖和側視圖都是半徑為$\sqrt{3}$的半圓和相同的正三角形,其中三角形的上頂點是半圓的中點,底邊在直徑上,則它的表面積是( )
如圖,某幾何體的三視圖中,正視圖和側視圖都是半徑為$\sqrt{3}$的半圓和相同的正三角形,其中三角形的上頂點是半圓的中點,底邊在直徑上,則它的表面積是( )| A. | 6π | B. | 8π | C. | 10π | D. | 11π |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 3 | B. | -3 | C. | -log36 | D. | -log38 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
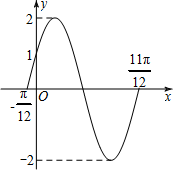 若y=f(x)=Asin(ωx+φ)(A>0,ω>0,$|φ|<\frac{π}{2})$的部分圖象如圖所示.
若y=f(x)=Asin(ωx+φ)(A>0,ω>0,$|φ|<\frac{π}{2})$的部分圖象如圖所示.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 是奇函數,不是偶函數 | B. | 是偶函數,不是奇函數 | ||
| C. | 既是奇函數數,又是偶函數 | D. | 既不是奇函數,也不是偶函數 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com