
【題目】已知在直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,點
,點![]() 在線段
在線段![]() 上.
上.

(Ⅰ)證明:![]() ;
;
(Ⅱ)求平面![]() 與平面
與平面![]() 所成銳二面角的余弦值.
所成銳二面角的余弦值.
【答案】(I)證明見解析;(II)![]() .
.
【解析】
試題分析:(1)根據(jù)邊角關(guān)系得到![]() ,進而得到
,進而得到![]() ,
,![]() ,
,![]() ,∴
,∴![]() ,又因為是直三棱柱,故
,又因為是直三棱柱,故![]() ,進而得到線線垂直;(2)建立坐標系,求平面
,進而得到線線垂直;(2)建立坐標系,求平面![]() 的法向量
的法向量![]() ,平面
,平面![]() 的法向量
的法向量![]() ,根據(jù)向量夾角的求法得到余弦值.
,根據(jù)向量夾角的求法得到余弦值.
解析:
(Ⅰ)不妨設(shè)![]() ,則
,則![]() ,
,![]() ,
,![]() ,
,![]() .
.
在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]()
![]() ,∴
,∴![]() ,即
,即![]() ;
;
∵![]() ,
,![]() ,∴
,∴![]() ,
,
∵![]() 為直三棱柱,∴
為直三棱柱,∴![]() 平面
平面![]() ,∴
,∴![]() ;
;
∴![]() 平面
平面![]() ,∵點
,∵點![]() 在線段
在線段![]() 上,∴
上,∴![]() .
.
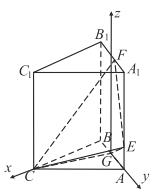
(Ⅱ)由(Ⅰ)知,![]() 平面
平面![]() ,建立如圖所示的空間直角坐標系
,建立如圖所示的空間直角坐標系![]() ,
,
不妨設(shè)![]() ,則
,則![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,
,![]() ,
,![]() .
.
設(shè)平面![]() 的法向量
的法向量![]() ,則
,則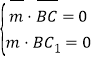 ,
,
即![]() ,取
,取![]() ,則
,則![]() ,
,![]() ,
,
則平面![]() 的一個法向量
的一個法向量![]() ;
;
設(shè)平面![]() 的法向量
的法向量![]() ,則
,則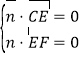 ,即
,即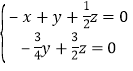 ,
,
取![]() ,則
,則![]() ,
,![]() ,則平面
,則平面![]() 的一個法向量
的一個法向量![]() ;
;
∴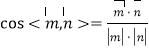
![]() ,
,
故平面![]() 與平面
與平面![]() 所成銳二面角的余弦值為
所成銳二面角的余弦值為![]() .
.


 計算高手系列答案
計算高手系列答案科目:高中數(shù)學 來源: 題型:
【題目】甲、乙、丙、丁四位同學中僅有一人申請了北京大學的自主招生考試,當他們被問到誰申請了北京大學的自主招生考試時,甲說:“丙或丁申請了”;乙說:“丙申請了”;丙說:“甲和丁都沒有申請”;丁說:“乙申請了”,如果這四位同學中只有兩人說的是對的,那么申請了北京大學的自主招生考試的同學是______.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ,其中
,其中![]() ;
;
(Ⅰ)若函數(shù)![]() 在
在![]() 處取得極值,求實數(shù)
處取得極值,求實數(shù)![]() 的值,
的值,
(Ⅱ)在(Ⅰ)的結(jié)論下,若關(guān)于![]() 的不等式
的不等式![]() ,當
,當![]() 時恒成立,求
時恒成立,求![]() 的值.
的值.
(Ⅲ)令![]() ,若關(guān)于
,若關(guān)于![]() 的方程
的方程![]() 在
在![]() 內(nèi)至少有兩個解,求出實數(shù)
內(nèi)至少有兩個解,求出實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某市為了引導居民合理用水,居民生活用水實行二級階梯式水價計量辦法,具體如下:第一階梯,每戶居民月用水量不超過12噸,價格為4元/噸;第二階梯,每戶居民月用水量超過12噸,超過部分的價格為8元/噸.為了了解全市居民月用水量的分布情況,通過抽樣獲得了100戶居民的月用水量(單位:噸),將數(shù)據(jù)按照![]() ,
, ![]() ,…,
,…, ![]() 分成8組,制成了如圖1所示的頻率分布直方圖.
分成8組,制成了如圖1所示的頻率分布直方圖.
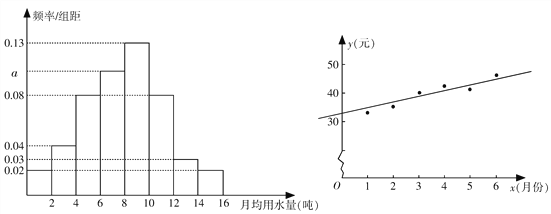
(圖1) (圖2)
(Ⅰ)求頻率分布直方圖中字母![]() 的值,并求該組的頻率;
的值,并求該組的頻率;
(Ⅱ)通過頻率分布直方圖,估計該市居民每月的用水量的中位數(shù)![]() 的值(保留兩位小數(shù));
的值(保留兩位小數(shù));
(Ⅲ)如圖2是該市居民張某2016年1~6月份的月用水費![]() (元)與月份
(元)與月份![]() 的散點圖,其擬合的線性回歸方程是
的散點圖,其擬合的線性回歸方程是![]() . 若張某2016年1~7月份水費總支出為312元,試估計張某7月份的用水噸數(shù).
. 若張某2016年1~7月份水費總支出為312元,試估計張某7月份的用水噸數(shù).
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知![]() 的直角頂點
的直角頂點![]() 在
在![]() 軸上,點
軸上,點![]() ,
,![]() 為斜邊
為斜邊![]() 的中點,且
的中點,且![]() 平行于
平行于![]() 軸.
軸.
(1)求點![]() 的軌跡方程;
的軌跡方程;
(2)設(shè)點![]() 的軌跡為曲線
的軌跡為曲線![]() ,直線
,直線![]() 與
與![]() 的另一個交點為
的另一個交點為![]() .以
.以![]() 為直徑的圓交
為直徑的圓交![]() 軸于
軸于![]() 、
、![]() ,記此圓的圓心為
,記此圓的圓心為![]() ,
,![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() 的離心率為
的離心率為![]() ,且橢圓
,且橢圓![]() 過點
過點 .過點
.過點![]() 做兩條相互垂直的直線
做兩條相互垂直的直線![]() 、
、![]() 分別與橢圓
分別與橢圓![]() 交于
交于![]() 、
、![]() 、
、![]() 、
、![]() 四點.
四點.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)若![]() ,
, ![]() ,探究:直線
,探究:直線![]() 是否過定點?若是,請求出定點坐標;若不是,請說明理由.
是否過定點?若是,請求出定點坐標;若不是,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]()
(1)討論函數(shù)f(x)的極值點的個數(shù);
(2)若f(x)有兩個極值點x1、x2,證明:f(x1)+f(x2)>3-4ln2.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,已知圓![]() ,拋物線
,拋物線![]() 的頂點為
的頂點為![]() ,準線的方程為
,準線的方程為![]() ,
,![]() 為拋物線
為拋物線![]() 上的動點,過點
上的動點,過點![]() 作圓
作圓![]() 的兩條切線與
的兩條切線與![]() 軸交于
軸交于![]() .
.

(Ⅰ)求拋物線![]() 的方程;
的方程;
(Ⅱ)若![]() ,求△
,求△![]() 面積
面積![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com