
【題目】已知函數![]() ,
, ![]() .
.
(Ⅰ)當![]() 時,求曲線
時,求曲線![]() 在
在![]() 處的切線方程;
處的切線方程;
(Ⅱ)求函數![]() 在
在![]() 上的最小值;
上的最小值;
(Ⅲ)若函數![]() ,當
,當![]() 時,
時, ![]() 的最大值為
的最大值為![]() ,求證:
,求證: ![]() .
.
【答案】(Ⅰ)![]() (Ⅱ)見解析;(Ⅲ)見解析.
(Ⅱ)見解析;(Ⅲ)見解析.
【解析】試題分析:(Ⅰ)由題![]() ,
, ![]()
所以![]() 故
故![]() ,
, ![]() ,代入點斜式可得曲線
,代入點斜式可得曲線![]() 在
在![]() 處的切線方程;
處的切線方程;
(Ⅱ)由題![]()
(1)當![]() 時,
時, ![]() 在
在![]() 上單調遞增. 則函數
上單調遞增. 則函數![]() 在
在![]() 上的最小值是
上的最小值是![]()
(2)當![]() 時,令
時,令![]() ,即
,即![]() ,令
,令![]() ,即
,即![]()
(i)當![]() ,即
,即![]() 時,
時, ![]() 在
在![]() 上單調遞增,
上單調遞增,
所以![]() 在
在![]() 上的最小值是
上的最小值是![]()
(ii)當![]() ,即
,即![]() 時,由
時,由![]() 的單調性可得
的單調性可得![]() 在
在![]() 上的最小值是
上的最小值是![]()
(iii)當![]() ,即
,即![]() 時,
時, ![]() 在
在![]() 上單調遞減,
上單調遞減, ![]() 在
在![]() 上的最小值是
上的最小值是![]()
(Ⅲ)![]() 當
當![]() 時,
時, ![]()
令![]() ,則
,則![]() 是單調遞減函數.
是單調遞減函數.
因為![]() ,
, ![]() ,
,
所以在![]() 上存在
上存在![]() ,使得
,使得![]() ,即
,即![]()
討論可得![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減.
上單調遞減.
所以當![]() 時,
時, ![]() 取得最大值是
取得最大值是![]()
因為![]() ,所以
,所以 由此可證
由此可證![]()
試題解析:(Ⅰ)因為函數![]() ,且
,且![]() ,
,
所以![]() ,
, ![]()
所以![]()
所以![]() ,
, ![]()
所以曲線在![]() 處的切線方程是
處的切線方程是![]() ,即
,即![]()
(Ⅱ)因為函數![]() ,所以
,所以![]()
(1)當![]() 時,
時, ![]() ,所以
,所以![]() 在
在![]() 上單調遞增.
上單調遞增.
所以函數![]() 在
在![]() 上的最小值是
上的最小值是![]()
(2)當![]() 時,令
時,令![]() ,即
,即![]() ,所以
,所以![]()
令![]() ,即
,即![]() ,所以
,所以![]()
(i)當![]() ,即
,即![]() 時,
時, ![]() 在
在![]() 上單調遞增,
上單調遞增,
所以![]() 在
在![]() 上的最小值是
上的最小值是![]()
(ii)當![]() ,即
,即![]() 時,
時, ![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,
上單調遞增,
所以![]() 在
在![]() 上的最小值是
上的最小值是![]()
(iii)當![]() ,即
,即![]() 時,
時, ![]() 在
在![]() 上單調遞減,
上單調遞減,
所以![]() 在
在![]() 上的最小值是
上的最小值是![]()
綜上所述,當![]() 時,
時, ![]() 在
在![]() 上的最小值是
上的最小值是![]()
當![]() 時,
時, ![]() 在
在![]() 上的最小值是
上的最小值是![]()
當![]() 時,
時, ![]() 在
在![]() 上的最小值是
上的最小值是![]()
(Ⅲ)因為函數![]() ,所以
,所以![]()
所以當![]() 時,
時, ![]()
令![]() ,所以
,所以![]() 是單調遞減函數.
是單調遞減函數.
因為![]() ,
, ![]() ,
,
所以在![]() 上存在
上存在![]() ,使得
,使得![]() ,即
,即![]()
所以當![]() 時,
時, ![]() ;當
;當![]() 時,
時, ![]()
即當![]() 時,
時, ![]() ;當
;當![]() 時,
時, ![]()
所以![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減.
上單調遞減.
所以當![]() 時,
時, ![]() 取得最大值是
取得最大值是![]()
因為![]() ,所以
,所以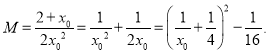
因為![]() ,所以
,所以![]()
所以![]()


科目:高中數學 來源: 題型:
【題目】已知點![]() ,
,![]() 分別在
分別在![]() 軸,
軸,![]() 軸上運動,
軸上運動,![]() ,點
,點![]() 在線段
在線段![]() 上,且
上,且![]() .
.
(1)求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)直線![]() 與
與![]() 交于
交于![]() ,
,![]() 兩點,
兩點,![]() ,若直線
,若直線![]() ,
,![]() 的斜率之和為2,直線
的斜率之和為2,直線![]() 是否恒過定點?若是,求出定點的坐標;若不是,請說明理由.
是否恒過定點?若是,求出定點的坐標;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在四棱錐S—ABCD中,底面ABCD為長方形,SB⊥底面ABCD,其中BS=2,BA=2,BC=λ,λ的可能取值為:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤λ=3
;⑤λ=3

(1)求直線AS與平面ABCD所成角的正弦值;
(2)若線段CD上能找到點E,滿足AE⊥SE,則λ可能的取值有幾種情況?請說明理由;
(3)在(2)的條件下,當λ為所有可能情況的最大值時,線段CD上滿足AE⊥SE的點有兩個,分別記為E1,E2,求二面角E1-SB-E2的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某校舉行的航天知識競賽中,參與競賽的文科生與理科生人數之比為![]() ,且成績分布在
,且成績分布在![]() ,分數在
,分數在![]() 以上(含
以上(含![]() )的同學獲獎. 按文理科用分層抽樣的方法抽取
)的同學獲獎. 按文理科用分層抽樣的方法抽取![]() 人的成績作為樣本,得到成績的頻率分布直方圖(見下圖).
人的成績作為樣本,得到成績的頻率分布直方圖(見下圖).
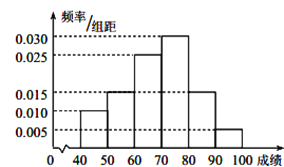
(I)在答題卡上填寫下面的![]() 列聯表,能否有超過
列聯表,能否有超過![]() 的把握認為“獲獎與學生的文理科有關”?
的把握認為“獲獎與學生的文理科有關”?
文科生 | 理科生 | 合計 | |
獲獎 |
| ||
不獲獎 | |||
合計 |
|
(II)將上述調査所得的頻率視為概率,現從該校參與競賽的學生中,任意抽取![]() 名學生,記“獲獎”學生人數為
名學生,記“獲獎”學生人數為![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
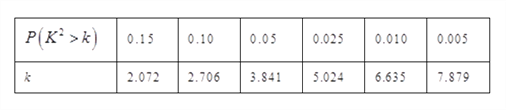
附表及公式:,其中
![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著銀行業的不斷發展,市場競爭越來越激烈,顧客對銀行服務質量的要求越來越高,銀行為了提高柜員員工的服務意識,加強評價管理,工作中讓顧客對服務作出評價,評價分為滿意、基本滿意、不滿意三種.某銀行為了比較顧客對男女柜員員工滿意度評價的差異,在下屬的四個分行中隨機抽出40人(男女各半)進行分析比較.對40人一月中的顧客評價“不滿意”的次數進行了統計,按男、女分為兩組,再將每組柜員員工的月“不滿意”次數分為5組:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到如下頻數分布表.
,得到如下頻數分布表.
分組 |
|
|
|
|
|
女柜員 | 2 | 3 | 8 | 5 | 2 |
男柜員 | 1 | 3 | 9 | 4 | 3 |
(1)在答題卡所給的坐標系中分別畫出男、女柜員員工的頻率分布直方圖;分別求出男、女柜員員工的月平均“不滿意”次數的估計值,試根據估計值比較男、女柜員員工的滿意度誰高?
(2)在抽取的40名柜員員工中:從“不滿意”次數不少于20的員工中隨機抽取3人,并用X表示隨機抽取的3人中女柜員工的人數,求X的分布列和數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com