
【題目】隨著銀行業的不斷發展,市場競爭越來越激烈,顧客對銀行服務質量的要求越來越高,銀行為了提高柜員員工的服務意識,加強評價管理,工作中讓顧客對服務作出評價,評價分為滿意、基本滿意、不滿意三種.某銀行為了比較顧客對男女柜員員工滿意度評價的差異,在下屬的四個分行中隨機抽出40人(男女各半)進行分析比較.對40人一月中的顧客評價“不滿意”的次數進行了統計,按男、女分為兩組,再將每組柜員員工的月“不滿意”次數分為5組:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到如下頻數分布表.
,得到如下頻數分布表.
分組 |
|
|
|
|
|
女柜員 | 2 | 3 | 8 | 5 | 2 |
男柜員 | 1 | 3 | 9 | 4 | 3 |
(1)在答題卡所給的坐標系中分別畫出男、女柜員員工的頻率分布直方圖;分別求出男、女柜員員工的月平均“不滿意”次數的估計值,試根據估計值比較男、女柜員員工的滿意度誰高?
(2)在抽取的40名柜員員工中:從“不滿意”次數不少于20的員工中隨機抽取3人,并用X表示隨機抽取的3人中女柜員工的人數,求X的分布列和數學期望.
【答案】(1)直方圖見解析;男、女柜員月平均“不滿意”次數的估計值分別為![]() ,
,![]() ;女柜員員工的滿意度高;(2)分布列見解析,
;女柜員員工的滿意度高;(2)分布列見解析,![]()
【解析】
(1)分別列出女柜員、男柜員的頻率分布表,再畫出女柜員、男柜員的頻率分布直方圖;計算女柜員、男柜員員工的月平均“不滿意”次數,比較即可得出結論.
(2)在抽取的40名柜員員工中,“不滿意”次數不少于20的柜員員工共有5人,其中女員工2人,男員工3人,從“不滿意”次數不少于20的柜員員工中隨機抽取3人,故X的所有可能取值為0,1,2,分別寫出分布列,求出數學期望值.
(1)對于女柜員列出頻率分布表如下,
分組 | [0,5) | [5,10) | [10,15) | [15,20) | [20,25] |
女柜員 | 2 | 3 | 8 | 5 | 2 |
頻率 | 0.1 | 0.15 | 0.4 | 0.25 | .0.1 |
對于男柜員列出頻率分布表如下;
分組 | [0,5) | [5,10) | [10,15) | [15,20) | [20,25] |
男柜員 | 1 | 3 | 9 | 4 | 3 |
男柜員 | 0.05 | 0.15 | 0.45 | 0.2 | 0.15 |
分別求出每組的頻率,畫出的直方圖如圖.
女柜員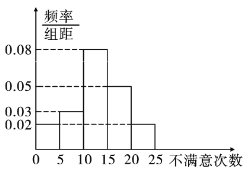 男柜員
男柜員 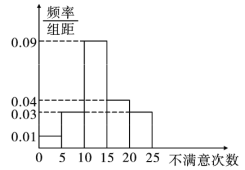
設女、男柜員員工的月平均“不滿意”次數分別為![]() ,
,![]() ,
,
則![]() ,
,
![]() ,
,
![]() ,所以女柜員員工的滿意度比男柜員員工的滿意度要高.
,所以女柜員員工的滿意度比男柜員員工的滿意度要高.
(2)在抽取的40名柜員員工中,“不滿意”次數不少于20的柜員員工共有5人,其中女員工2人,男員工3人,
從“不滿意”次數不少于20的柜員員工中隨機抽取3人,故X的所有可能取值為0,1,2,
則![]() ,
,![]() ,
,![]() ,
,
所以X的分布列為
X | 0 | 1 | 2 |
P |
|
|
|
所以![]() .
.


科目:高中數學 來源: 題型:
【題目】中學為研究學生的身體素質與體育鍛煉時間的關系,對該校200名高三學生平均每天體育鍛煉時間進行調查,如表:(平均每天鍛煉的時間單位:分鐘)
平均每天鍛煉的時間/分鐘 |
|
|
|
|
|
|
總人數 | 20 | 36 | 44 | 50 | 40 | 10 |
將學生日均體育鍛煉時間在![]() 的學生評價為“鍛煉達標”.
的學生評價為“鍛煉達標”.
(1)請根據上述表格中的統計數據填寫下面的![]() 列聯表;
列聯表;
鍛煉不達標 | 鍛煉達標 | 合計 | |
男 | |||
女 | 20 | 110 | |
合計 |
并通過計算判斷,是否能在犯錯誤的概率不超過0.025的前提下認為“鍛煉達標”與性別有關?
(2)在“鍛煉達標”的學生中,按男女用分層抽樣方法抽出10人,進行體育鍛煉體會交流,
(i)求這10人中,男生、女生各有多少人?
(ii)從參加體會交流的10人中,隨機選出2人作重點發言,記這2人中女生的人數為![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
參考公式:![]() ,其中
,其中![]() .
.
臨界值表
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校為了選拔學生參加“XX市中學生知識競賽”,先在本校進行選拔測試,若該校有100名學生參加選拔測試,并根據選拔測試成績作出如圖所示的頻率分布直方圖.
(1)根據頻率分布直方圖,估算這100名學生參加選拔測試的平均成績;
(2)該校推薦選拔測試成績在110以上的學生代表學校參加市知識競賽,為了了解情況,在該校推薦參加市知識競賽的學生中隨機抽取2人,求選取的兩人的選拔成績在頻率分布直方圖中處于不同組的概率.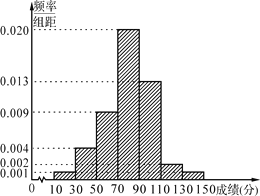
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】每年六、七月份,我國長江中下游地區進入持續25天左右的梅雨季節,如圖是江南某地區![]() 年10年間梅雨季節的降雨量
年10年間梅雨季節的降雨量![]() 單位:
單位:![]() 的頻率分布直方圖,試用樣本頻率估計總體概率,解答下列問題:
的頻率分布直方圖,試用樣本頻率估計總體概率,解答下列問題:

![]() 假設每年的梅雨季節天氣相互獨立,求該地區未來三年里至少有兩年梅雨季節的降雨量超過350mm的概率.
假設每年的梅雨季節天氣相互獨立,求該地區未來三年里至少有兩年梅雨季節的降雨量超過350mm的概率.
![]() 老李在該地區承包了20畝土地種植楊梅,他過去種植的甲品種楊梅,平均每年的總利潤為28萬元
老李在該地區承包了20畝土地種植楊梅,他過去種植的甲品種楊梅,平均每年的總利潤為28萬元![]() 而乙品種楊梅的畝產量
而乙品種楊梅的畝產量![]() 畝
畝![]() 與降雨量之間的關系如下面統計表所示,又知乙品種楊梅的單位利潤為
與降雨量之間的關系如下面統計表所示,又知乙品種楊梅的單位利潤為![]() 元
元![]() ,請你幫助老李分析,他來年應該種植哪個品種的楊梅可以使總利潤
,請你幫助老李分析,他來年應該種植哪個品種的楊梅可以使總利潤![]() 萬元
萬元![]() 的期望更大?并說明理由.
的期望更大?并說明理由.
降雨量 |
|
|
|
|
畝產量 | 500 | 700 | 600 | 400 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平行六面體ABCD-A1B1C1D1中,AA1⊥平面ABCD,且AB=AD=2,AA1=![]() ,∠BAD=120°.
,∠BAD=120°.
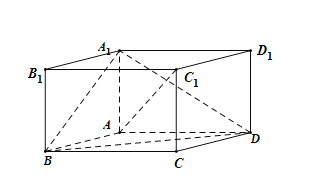
(1)求異面直線A1B與AC1所成角的余弦值;
(2)求二面角B-A1D-A的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地政府為了幫助當地農民脫貧致富,開發了一種新型水果類食品,該食品生產成本為每件8元.當天生產當天銷售時,銷售價為每件12元,當天未賣出的則只能賣給水果罐頭廠,每件只能賣5元.每天的銷售量與當天的氣溫有關,根據市場調查,若氣溫不低于![]() ,則銷售5000件;若氣溫位于
,則銷售5000件;若氣溫位于![]() ,則銷售3500件;若氣溫低于
,則銷售3500件;若氣溫低于![]() ,則銷售2000件.為制定今年8月份的生產計劃,統計了前三年8月份的氣溫范圍數據,得到下面的頻數分布表:
,則銷售2000件.為制定今年8月份的生產計劃,統計了前三年8月份的氣溫范圍數據,得到下面的頻數分布表:
氣溫范圍 (單位: |
|
|
|
|
|
天數 | 4 | 14 | 36 | 21 | 15 |
以氣溫范圍位于各區間的頻率代替氣溫范圍位于該區間的概率.
(1)求今年8月份這種食品一天銷售量(單位:件)的分布列和數學期望值;
(2)設8月份一天銷售這種食品的利潤為![]() (單位:元),當8月份這種食品一天生產量
(單位:元),當8月份這種食品一天生產量![]() (單位:件)為多少時,
(單位:件)為多少時,![]() 的數學期望值最大,最大值為多少
的數學期望值最大,最大值為多少![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com