
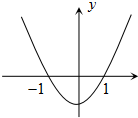
 設f(x)=ax3+bx2+cx的極小值為-2,其導函數y=f′(x)的圖象是經過點(-1,0),(1,0)開口向上的拋物線,如圖所示.
設f(x)=ax3+bx2+cx的極小值為-2,其導函數y=f′(x)的圖象是經過點(-1,0),(1,0)開口向上的拋物線,如圖所示.分析 (1)觀察圖象滿足f′(x)=0的點附近的導數的符號的變化情況,來確定極小值,根據圖象可得f'(1)=0,f'(1)=0,f(1)=-2,即可求出a,b,c的值,
(2)先將過點A(1,m)(m≠-2)可作曲線y=f(x)的三條切線轉化為:方程2x3-3x2+m+3=0(*)有三個不同實數根,記g(x)=2x3-3x2+m+3,g'(x)=6x2-6x=6x(x-1),下面利用導數研究函數g(x)的零點,從而求得m的范圍
解答 解:(1)由圖象可知,在(-∞,1)上f'(x)>0,在(-1,1)上f'(x)<0.在(1,+∞)上f'(x)>0.
故f(x)在(-∞,1),(1,+∞)上遞增,在(-1,1)上遞減.
因此f(x)在x=1處取得極小值,
∴f(1)=a+b+c=-2
∵f'(x)=3ax2+2bx+c,
∴f'(-1)=0,f'(1)=0,
∴-1+1=$\frac{-2b}{3a}$,即b=0,-1×1=$\frac{c}{3a}$,即c=-3a,
∴a=1,b=0,c=-3,
∴f(x)=x3-3x,
(2)過點A(1,m)向曲線y=f(x)作切線,設切點為(x0,y0)
則y0=x03-3x0,k=f'(x0)=3x02-3.
則切線方程為y-(x03-3x0)=(3x02-3)(x-x0)
將A(1,m)代入上式,整理得2x03-3x02+m+3=0.
∵過點A(1,m)(m≠-2)可作曲線y=f(x)的三條切線
∴方程2x3-3x2+m+3=0(*)有三個不同實數根、
記g(x)=2x3-3x2+m+3,g'(x)=6x2-6x=6x(x-1)、
令g'(x)=0,x=0或1、
則x,g'(x),g(x)的變化情況如下表
| x | (-∞,0) | 0 | (0,1) | 1 | (1,+∞) |
| g'(x) | + | 0 | - | 0 | + |
| g(x) | 遞增 | 極大 | 遞減 | 極小 | 遞增 |
點評 本題主要考查了利用導數研究函數的極值、單調性,以及觀察圖形的能力、運算求解能力,考查數形結合思想、化歸與轉化思想.屬于中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | [-1,2] | B. | [1,+∞) | C. | (-∞,-2]∪[1,+∞) | D. | [-2,1] |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | a<1 | B. | a≤1 | C. | a<2 | D. | a≤2 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{6}$ | B. | $\sqrt{10}$ | C. | 2$\sqrt{2}$ | D. | 4 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com