
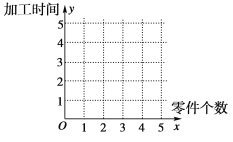
【題目】某車間為了規(guī)定工時定額,需要確定加工零件所花費(fèi)的時間,為此作了四次試驗(yàn),得到的數(shù)據(jù)如下:
零件的個數(shù) | 2 | 3 | 4 | 5 |
加工的時間 | 2.5 | 3 | 4 | 4.5 |
(1)在給定的坐標(biāo)系中畫出表中數(shù)據(jù)的散點(diǎn)圖;
(2)求出![]() 關(guān)于
關(guān)于![]() 的線性回歸方程
的線性回歸方程![]() ,并在坐標(biāo)系中畫出回歸直線;
,并在坐標(biāo)系中畫出回歸直線;
(3)試預(yù)測加工![]() 個零件需要多少時間?
個零件需要多少時間?
參考公式:回歸直線![]() ,其中
,其中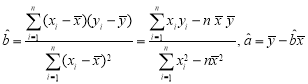 .
.
【答案】(1)見圖;(2)線性回歸方程為![]() ,回歸直線見圖;(3)預(yù)測加工
,回歸直線見圖;(3)預(yù)測加工![]() 個零件需要
個零件需要![]() 小時.
小時.

【解析】
試題分析:(1)畫散點(diǎn)圖,即根據(jù)提供的數(shù)對,找出對應(yīng)的點(diǎn)即可,這一點(diǎn)不難;(2)首先要了解提供的計算公式中每個部分的含義,然后分步計算,這樣做的好處在于出錯時便于檢查是哪步出錯了,也能分步得分;(3)若了解回歸方程的意義和作用,此問也不難,這一題對回歸分析這部分內(nèi)容考查的比較全面,其實(shí)關(guān)鍵還是落實(shí)在知識的理解和計算能力上.
試題解析:(1)散點(diǎn)圖如下圖.
 3分
3分
(2)由表中數(shù)據(jù)得![]() ,
,![]() ,
,![]() ,
,![]()
所以 ,
,![]() 9分
9分
因此![]() 回歸直線如圖中所示. 10分
回歸直線如圖中所示. 10分
(3)將![]() 代入回歸直線方程,得
代入回歸直線方程,得![]() (小時),
(小時),
∴預(yù)測加工![]() 個零件需要
個零件需要![]() 小時. 12分
小時. 12分



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】中央政府為了應(yīng)對因人口老齡化而造成的勞動力短缺等問題,擬定出臺“延遲退休年齡政策”.為了了解人們對“延遲退休年齡政策”的態(tài)度,責(zé)成人社部進(jìn)行調(diào)研.人社部從網(wǎng)上年齡在15~65歲的人群中隨機(jī)調(diào)查100人,調(diào)查數(shù)據(jù)的頻率分布直方圖如圖所示, 支持“延遲退休年齡政策”的人數(shù)與年齡的統(tǒng)計結(jié)果如表:

年齡(歲) |
|
|
|
|
|
支持“延遲退休年齡政策”人數(shù) | 15 | 5 | 15 | 28 | 17 |
(I)由以上統(tǒng)計數(shù)據(jù)填寫下面的![]() 列聯(lián)表;
列聯(lián)表;
年齡低于45歲的人數(shù) | 年齡不低于45歲的人數(shù) | 總計 | |
支持 | |||
不支持 | |||
總計 |
(II)通過計算判斷是否有![]() 的把握認(rèn)為以45歲為分界點(diǎn)的不同人群對“延遲退休年齡政策”的態(tài)度有差異.
的把握認(rèn)為以45歲為分界點(diǎn)的不同人群對“延遲退休年齡政策”的態(tài)度有差異.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
參考公式:![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】一個口袋中有![]() 個白球和
個白球和![]() 個紅球(
個紅球(![]() ,且
,且![]() ),每次從袋中摸出兩個球(每次摸球后把這兩個球放回袋中),若摸出的兩個球顏色相同為中獎,否則為不中獎.
),每次從袋中摸出兩個球(每次摸球后把這兩個球放回袋中),若摸出的兩個球顏色相同為中獎,否則為不中獎.
(1)試用含![]() 的代數(shù)式表示一次摸球中獎的概率
的代數(shù)式表示一次摸球中獎的概率![]() ;
;
(2)若![]() ,求三次摸球恰有一次中獎的概率;
,求三次摸球恰有一次中獎的概率;
(3)記三次摸球恰有一次中獎的概率為![]() ,當(dāng)
,當(dāng)![]() 為何值時,
為何值時,![]() 取最大值.
取最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
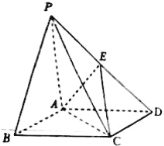
【題目】如圖,在四棱錐P—ABCD中,底面ABCD是菱形,∠ABC=60°,PA=AC,PB=PD=![]() AC,E是PD的中點(diǎn),求證:
AC,E是PD的中點(diǎn),求證:
(1)PB∥平面ACE;
(2)平面PAC⊥平面ABCD.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
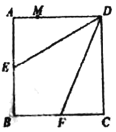
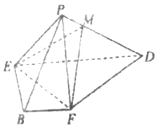
【題目】如圖,在正方形![]() 中,點(diǎn)
中,點(diǎn)![]() 是
是![]() 的中點(diǎn),點(diǎn)
的中點(diǎn),點(diǎn)![]() 是
是![]() 的中點(diǎn),將
的中點(diǎn),將![]() 分別沿
分別沿![]() 折起,使
折起,使![]() 兩點(diǎn)重合于
兩點(diǎn)重合于![]() ,連接
,連接![]() .
.
(1)求證:![]() ;
;
(2)點(diǎn)![]() 是
是![]() 上一點(diǎn),若
上一點(diǎn),若![]() 平面
平面![]() ,則
,則![]() 為何值?并說明理由.
為何值?并說明理由.
(3)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,正方體![]() 的棱長為
的棱長為![]() ,
, ![]() 分別是
分別是![]() 的中點(diǎn),點(diǎn)
的中點(diǎn),點(diǎn)![]() 在棱
在棱![]()
上, ![]() (
(![]() ).
).

(Ⅰ)三棱錐![]() 的體積分別為
的體積分別為![]() ,當(dāng)
,當(dāng)![]() 為何值時,
為何值時, ![]() 最大?最大值為多少?
最大?最大值為多少?
(Ⅱ)若![]() 平面
平面![]() ,證明:平面
,證明:平面![]() 平面
平面![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】 如圖,在四棱錐![]() 中,底面
中,底面![]() 為平行四邊形,
為平行四邊形,![]() 為等邊三角形,平面
為等邊三角形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,

(Ⅰ)設(shè)![]() 分別為
分別為![]() 的中點(diǎn),求證:
的中點(diǎn),求證:![]() 平面
平面![]() ;
;
(Ⅱ)求證:![]() 平面
平面![]() ;
;
(Ⅲ)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】用五種不同顏色給三棱臺![]() 的六個頂點(diǎn)染色,要求每個點(diǎn)染一種顏色,且每條棱的兩個端點(diǎn)染不同顏色.則不同的染色方法有___________種.
的六個頂點(diǎn)染色,要求每個點(diǎn)染一種顏色,且每條棱的兩個端點(diǎn)染不同顏色.則不同的染色方法有___________種.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com