
分析 先求出向量$\overrightarrow{AB}$,$\overrightarrow{CD}$,利用cos<$\overrightarrow{AB},\overrightarrow{CD}$>=$\frac{\overrightarrow{AB}•\overrightarrow{CD}}{|\overrightarrow{AB}|•|\overrightarrow{CD}|}$,能求出向量$\overrightarrow{AB}$與$\overrightarrow{CD}$的夾角的余弦值.
解答 解:∵點A(-1,0,1),B(0,0,1),C(2,2,2),D(0,0,3),
∴$\overrightarrow{AB}$=(1,0,0),$\overrightarrow{CD}$=(-2,-2,1),
∴cos<$\overrightarrow{AB},\overrightarrow{CD}$>=$\frac{\overrightarrow{AB}•\overrightarrow{CD}}{|\overrightarrow{AB}|•|\overrightarrow{CD}|}$=$\frac{-2}{1×\sqrt{9}}$=-$\frac{2}{3}$.
∴向量$\overrightarrow{AB}$與$\overrightarrow{CD}$的夾角的余弦值為-$\frac{2}{3}$.
點評 本題考查向量夾角的余弦值的求法,考查空間向量坐標運算法則、空間向量夾角余弦值計算公式等基礎知識,考查推理論證能力、運算求解能力,考查化歸與轉化思想,是基礎題.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ?x1,x2∈R,(f(x1)-f(x2))(x1-x2)>0 | B. | ?x1,x2∈R,(f(x1)-f(x2))(x1-x2)≥0 | ||
| C. | ?x1,x2∈R,(f(x1)-f(x2))(x1-x2)≥0 | D. | ?x1,x2∈R,(f(x1)-f(x2))(x1-x2)<0 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
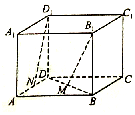 如圖所示,在正方體ABCD-A1B1C1D1中,已知棱長為a,M,N分別是BD和AD的中點,則B1M與D1N所成角的余弦值為( )
如圖所示,在正方體ABCD-A1B1C1D1中,已知棱長為a,M,N分別是BD和AD的中點,則B1M與D1N所成角的余弦值為( )| A. | $\frac{\sqrt{30}}{10}$ | B. | $\frac{\sqrt{30}}{10}$a | C. | -$\frac{\sqrt{30}}{10}$ | D. | $\frac{\sqrt{15}}{15}$a |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{5}{3}$ | B. | $\frac{\sqrt{41}}{4}$ | C. | $\frac{5}{4}$ | D. | $\frac{\sqrt{41}}{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [10,15] | B. | [12,17] | C. | [13,17] | D. | [15,17] |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com