
(本小題12分)設函數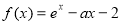 .
.
(1)求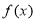 的單調區間;
的單調區間;
(2)若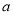 =1 ,
=1 ,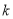 為整數,且當
為整數,且當
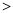 0時,
0時,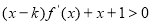 ,求
,求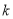 的最大值.
的最大值.
(1)若 ,則
,則 ,此時函數
,此時函數 在R上單調遞增;
在R上單調遞增;
若 ,則當
,則當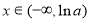 時,
時, ;當
;當 時,
時, .所以函數
.所以函數 在
在 上單調遞減;在
上單調遞減;在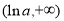 上單調遞增.
上單調遞增.
(2)整數 的最大值為2.
的最大值為2.
【解析】
試題分析:(1)首先根據函數 的表達式可判斷其定義域,然后對其進行求導可得
的表達式可判斷其定義域,然后對其進行求導可得 ,由于導函數中含有參數
,由于導函數中含有參數 ,將其分為兩種情況:①
,將其分為兩種情況:① ,此時易判斷出函數
,此時易判斷出函數 在R上單調遞增;②
在R上單調遞增;② ,可求出其極值點,然后判斷函數在極值點的左右兩側的單調性即可;
,可求出其極值點,然后判斷函數在極值點的左右兩側的單調性即可;
(2)首先將問題“當
 0時,
0時, ”轉化為“
”轉化為“ 恒成立,其中
恒成立,其中 ”,即
”,即 ,記
,記 ,求其導函數
,求其導函數 ,由(1)知,函數
,由(1)知,函數 在
在 上單調遞增,且在
上單調遞增,且在 上存在唯一的零點,即
上存在唯一的零點,即 在
在 上存在唯一的零點.從而得出函數
上存在唯一的零點.從而得出函數 的最小值并求出其取值范圍,進而得出整數
的最小值并求出其取值范圍,進而得出整數 的最大值.
的最大值.
試題解析:(1)函數 的定義域為R,所以
的定義域為R,所以 .
.
若 ,則
,則 ,此時函數
,此時函數 在R上單調遞增;
在R上單調遞增;
若 ,則當
,則當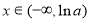 時,
時, ;當
;當 時,
時, .所以函數
.所以函數 在
在 上單調遞減;在
上單調遞減;在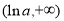 上單調遞增.
上單調遞增.
(2)因為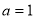 ,所以
,所以 ,所以當
,所以當 時,
時, 等價于
等價于 ,其中
,其中 .
.
令 ,則
,則 .
.
由(1)知,函數 在
在 上單調遞增,而
上單調遞增,而 ,
, ,所以
,所以 在
在 上存在唯一的零點,故
上存在唯一的零點,故 在
在 上存在唯一的零點.設此零點為
上存在唯一的零點.設此零點為 ,則
,則 .
.
當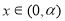 時,
時, ;當
;當 時,
時, ;所以
;所以 在
在 上的最小值為
上的最小值為 .又由
.又由 可得,
可得, ,所以
,所以 ,所以
,所以 ,故整數
,故整數 的最大值為2.
的最大值為2.
考點:1、利用導數判斷函數的單調性;2、導數在研究函數的最值中的應用.


科目:高中數學 來源:2015屆遼寧省五校協作體高三上學期期中考試文科數學試卷(解析版) 題型:選擇題
設l為直線,?,?是兩個不同的平面,下列命題中正確的是( )
A.若 ,
, ,則
,則
B.若 ,
, ,則
,則
C.若 ,
, ,則
,則
D.若 ,
, ,則
,則
查看答案和解析>>
科目:高中數學 來源:2015屆西藏拉薩中學高三第三次月考文科數學試卷(解析版) 題型:選擇題
已知數列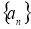 是等比數列,
是等比數列, 是其前
是其前 項和,且
項和,且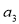 =2,
=2,  ,則
,則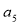 =
=
A.2或- B.
B.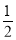 或-2 C.
或-2 C. D.2或
D.2或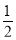
查看答案和解析>>
科目:高中數學 來源:2015屆福建省福州市高三上學期第三次質檢理科數學試卷(解析版) 題型:填空題
直線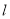 與函數
與函數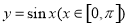 的圖像相切于點
的圖像相切于點 ,且
,且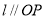 ,
, 為坐標原點,
為坐標原點,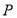 為圖像的極大值點,
為圖像的極大值點,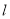 與
與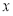 軸交于點
軸交于點 ,過切點
,過切點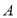 作
作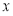 軸的垂線,垂足為
軸的垂線,垂足為 ,則
,則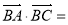 =__________.
=__________.
查看答案和解析>>
科目:高中數學 來源:2015屆福建省高三10月月考理科數學試卷(解析版) 題型:解答題
(本小題滿分13分)某沿海地區養殖的一種特色海鮮上市時間僅能持續5個月,預測上市初期和廂期會因供應不足使價格呈
持續上漲態勢,而中期又將出現供大于求使價格連續下跌.現有三種價格模擬函數:①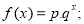 ②
②
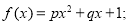 ③
③ (以上三式中
(以上三式中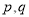 均為常數,且q>l).
均為常數,且q>l).
(1)為準確研究其價格走勢,應選哪種價格模擬函數(不必說明理由);
(2)若 ,求出所選函數
,求出所選函數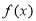 的解析式(注:函數定義域是
的解析式(注:函數定義域是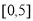 .其中
.其中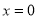 表示8
表示8
月1日,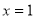 表示9月1日,…,以此類推);
表示9月1日,…,以此類推);
(3)在(2)的條件下研究下面課題:為保證養殖戶的經濟效益,當地政府計劃在價格下跌期間積極拓寬外銷,請你預測該海鮮將在哪幾個月份內價格下跌.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com