
【題目】已知函數![]() .
.
(1)若函數![]() 在
在![]() 處的切線方程為
處的切線方程為![]() ,求實數
,求實數![]() ,
,![]() 的值;
的值;
(2)若函數![]() 在
在![]() 和
和![]() 兩處取得極值,求實數
兩處取得極值,求實數![]() 的取值范圍;
的取值范圍;
(3)在(2)的條件下,若![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由題意得:![]() ,
,![]() ,解得
,解得![]() ,
,![]() .
.
(2)由題意知:![]() 有兩個零點
有兩個零點![]() ,
,![]() ,
,
令![]() ,而
,而![]() .
.
對![]() 時和
時和![]() 時分類討論,解得:
時分類討論,解得:![]() .經檢驗,合題;
.經檢驗,合題;
(3)由題意得,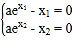 ,即
,即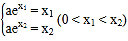 .
.
所以![]() ,令
,令![]() ,即
,即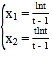 ,
,
令![]() ,求導,得
,求導,得![]() 在
在![]() 上單調遞減,即
上單調遞減,即![]() .
.
![]() ,
,![]() .令
.令![]() ,求導得
,求導得![]() 在
在![]() 上單調遞減,得
上單調遞減,得![]() 的取值范圍.
的取值范圍.
(1)![]() ,
,
由題意得:![]() ,即
,即![]() ,
,
![]() 即
即![]() ,所以
,所以![]() ,
,![]() .
.
(2)由題意知:![]() 有兩個零點
有兩個零點![]() ,
,![]() ,
,
令![]() ,而
,而![]() .
.
①當![]() 時,
時,![]() 恒成立
恒成立
所以![]() 單調遞減,此時
單調遞減,此時![]() 至多1個零點(舍).
至多1個零點(舍).
②當![]() 時,令
時,令![]() ,解得:
,解得:![]() ,
,
![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,
上單調遞增,
所以![]() ,
,
因為![]() 有兩個零點,所以
有兩個零點,所以![]() ,
,
解得:![]() .
.
因為![]() ,
,![]() ,且
,且![]() ,
,
而![]() 在
在![]() 上單調遞減,
上單調遞減,
所以![]() 在
在![]() 上有1個零點;
上有1個零點;
又因為![]() (易證
(易證![]() ),
),
則![]() 且
且![]() ,
,
而![]() 在
在![]() 上單調遞增,
上單調遞增,
所以![]() 在
在![]() 上有1個零點.
上有1個零點.
綜上:![]() .
.
(3)由題意得,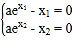 ,即
,即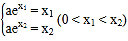 .
.
所以![]() ,令
,令![]() ,即
,即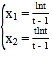 ,
,
令![]() ,
,![]() ,
,
令![]() ,而
,而![]() ,
,
所以![]() 在
在![]() 上單調遞減,即
上單調遞減,即![]() ,
,
所以![]() 在
在![]() 上單調遞減,即
上單調遞減,即![]() .
.
因為![]() ,
,![]() .
.
令![]() ,而
,而![]() 恒成立,
恒成立,
所以![]() 在
在![]() 上單調遞減,又
上單調遞減,又![]() ,
,
所以![]() .
.


 口算小狀元口算速算天天練系列答案
口算小狀元口算速算天天練系列答案 天天練口算系列答案
天天練口算系列答案科目:高中數學 來源: 題型:
【題目】已知在等比數列{an}中,![]() =2,,
=2,,![]() =128,數列{bn}滿足b1=1,b2=2,且{
=128,數列{bn}滿足b1=1,b2=2,且{![]() }為等差數列.
}為等差數列.
(1)求數列{an}和{bn}的通項公式;
(2)求數列{bn}的前n項和.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 的焦點為F,點P為拋物線C上一點,
的焦點為F,點P為拋物線C上一點,![]() ,O為坐標原點,
,O為坐標原點,![]() .
.
(1)求拋物線C的方程;
(2)設Q為拋物線C的準線上一點,過點F且垂直于OQ的直線交拋物線C于A,B兩點記![]() ,
,![]() 的面積分別為
的面積分別為![]()
![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知常數a≠0,數列![]() 的前n項和為
的前n項和為![]() ,且
,且![]()
(1)求證:數列![]() 為等差數列;
為等差數列;
(2)若![]() 且數列
且數列![]() 是單調遞增數列,求實數a的取值范圍;
是單調遞增數列,求實數a的取值范圍;
(3)若![]() 數列
數列![]() 滿足:
滿足: ![]() 對于任意給定的正整數k,是否存在p,
對于任意給定的正整數k,是否存在p,![]() ,使
,使![]() 若存在,求p,q的值(只要寫出一組即可);若不存在,說明理由.
若存在,求p,q的值(只要寫出一組即可);若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 的的參數方程為
的的參數方程為![]() (其中
(其中![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸的極坐標系中,點
軸的正半軸為極軸的極坐標系中,點![]() 的極坐標為
的極坐標為![]() ,直線
,直線![]() 經過點
經過點![]() .曲線
.曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的普通方程與曲線
的普通方程與曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)過點![]() 作直線
作直線![]() 的垂線交曲線
的垂線交曲線![]() 于
于![]() 兩點(
兩點(![]() 在
在![]() 軸上方),求
軸上方),求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 是拋物線
是拋物線![]() 的焦點,點
的焦點,點![]() 在
在![]() 軸上,
軸上,![]() 為坐標原點,且滿足
為坐標原點,且滿足![]() ,經過點
,經過點![]() 且垂直于
且垂直于![]() 軸的直線與拋物線
軸的直線與拋物線![]() 交于
交于![]() 、
、![]() 兩點,且
兩點,且![]() .
.
(1)求拋物線![]() 的方程;
的方程;
(2)直線![]() 與拋物線
與拋物線![]() 交于
交于![]() 、
、![]() 兩點,若
兩點,若![]() ,求點
,求點![]() 到直線
到直線![]() 的最大距離.
的最大距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】第七屆世界軍人運動會(以下簡稱武漢軍運會)專題新聞發布會在武漢舉行,武漢軍運會會徽、吉祥物正式公布.武漢軍運會將于![]() 年
年![]() 月
月![]() 日舉行,賽期
日舉行,賽期![]() 天.若將
天.若將![]() 名志愿者分配到兩個運動場館進行服務,每個運動場館至少
名志愿者分配到兩個運動場館進行服務,每個運動場館至少![]() 名志愿者,則其中志愿者甲、乙或甲、丙被分到同一場館的概率為______.
名志愿者,則其中志愿者甲、乙或甲、丙被分到同一場館的概率為______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的定義域為
的定義域為![]() ,若滿足
,若滿足![]() ,則稱函數
,則稱函數![]() 為“
為“![]() 型函數”.
型函數”.
(1)判斷函數![]() 和
和![]() 是否為“
是否為“![]() 型函數”,并說明理由;
型函數”,并說明理由;
(2)設函數![]() ,記
,記![]() 為函數
為函數![]() 的導函數.
的導函數.
①若函數![]() 的最小值為1,求
的最小值為1,求![]() 的值;
的值;
②若函數![]() 為“
為“![]() 型函數”,求
型函數”,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)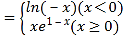 ,若關于x的方程f2(x)﹣af(x)+a﹣a2=0有四個不等的實數根,則a的取值范圍是( )
,若關于x的方程f2(x)﹣af(x)+a﹣a2=0有四個不等的實數根,則a的取值范圍是( )
A.![]() B.(﹣∞,﹣1)∪[1,+∞)
B.(﹣∞,﹣1)∪[1,+∞)
C.(﹣∞,﹣1)∪{1}D.(﹣1,0)∪{1}
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com