解:(I)當x>0時,sgn(x)=1,解方程x
2-3x+1=1,得x=0(舍)或x=3
當x=0時,sgn(x)=0,0不是方程x
2-3x+1=0的解
當x<0時,sgn(x)=-1,解方程x
2-3x+1=-1,得x=1(舍)或x=2(舍)
綜上所述,x=3是方程x
2-3x+1=sgn(x)的根.(3分)
(II)函數f(x)的定義域是{x|x>0}(4分)
當x>2時,f(x)=x-lnx,
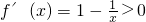
恒成立(5分)
當0<x<2時,f(x)=-(x-lnx),

解f'(x)>0得0<x<1或x>2(16分),
解f'(x)<0得1<x<2(7分)
綜上所述,函數f(x)=sgn(x-2)•(x-lnx)的單調增區間是(0,1),(2,+∞),單調減區間是(1,2).(8分)
( III)設點P(x,y)∈T,則(10
x,10
y)∈S.
于是有
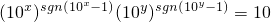
,
得x•sgn(10
x-1)+y•sgn(10
y-1)=1
當x>0時,10
x-1>0,sgn(10
x-1)=1,xsgn(10
x-1)=x
當x<0時,10
x-1<0,sgn(10
x-1)=-1,xsgn(10
x-1)=-x
∴xsgn(10
x-1)=|x|
同理,T={(x,y)||x|+|y|=1}(11分)
點集T圍成的區域是一個邊長為

的正方形,面積為2.(13分)
分析:(I)根據定義
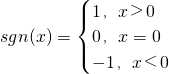
,對x進行討論,解一元二次方程即可求得結果;
(II)根據函數解析式求得函數的定義域{x|x>0},對x進行討論,求導,令導數大于零(小于零),解不等式即可求得函數的單調遞增(單調遞減)區間;
(III)根據定義求得點集TT={(x,y)||x|+|y|=1},從而點集T圍成的區域的面積.
點評:此題是個中檔題.考查分段函數分段處理,這是研究分段函數圖象和性質最核心的理念,具體做法是:分段函數的定義域、值域是各段上x、y取值范圍的并集,分段函數的奇偶性、單調性要在各段上分別論證;分段函數的最大值,是各段上最大值中的最大者,同時考查了學生分析問題和解決問題的能力和計算能力.

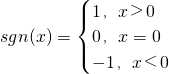 .
.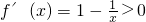 恒成立(5分)
恒成立(5分)
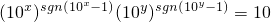 ,
, 的正方形,面積為2.(13分)
的正方形,面積為2.(13分)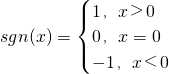 ,對x進行討論,解一元二次方程即可求得結果;
,對x進行討論,解一元二次方程即可求得結果;

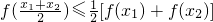 成立,則f(x)稱為I上的凹函數.
成立,則f(x)稱為I上的凹函數.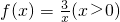 是否為凹函數?
是否為凹函數?