
【題目】拋物線![]() 和圓
和圓![]() ,直線
,直線![]() 與拋物線
與拋物線![]() 和圓
和圓![]() 分別交于四個點
分別交于四個點![]() (自下而上的順序為
(自下而上的順序為![]() ),則
),則![]() 的值為_________.
的值為_________.
科目:高中數學 來源: 題型:
【題目】已知動圓![]() 過定點
過定點![]() 且在
且在![]() 軸上截得的弦長為4。
軸上截得的弦長為4。
(1)求動圓![]() 的圓心
的圓心![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)過點![]() 的動直線與曲線
的動直線與曲線![]() 交于
交于![]() 兩點,點
兩點,點![]() 在曲線
在曲線![]() 上,使得
上,使得![]() 的重心
的重心![]() 在
在![]() 軸上,直線
軸上,直線![]() 交
交![]() 軸于點
軸于點![]() ,且點
,且點![]() 在點
在點![]() 的右側,記
的右側,記![]() 的面積為
的面積為![]() 的面積為
的面積為![]() ,求
,求![]() 的最小值。
的最小值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知過橢圓![]() 的左焦點
的左焦點![]() ,作斜率為
,作斜率為![]() 的直線
的直線![]() ,交橢圓
,交橢圓![]() 于
于![]() 兩點.
兩點.
(1)若原點![]() 到直線
到直線![]() 的距離為
的距離為![]() ,求直線
,求直線![]() 的方程;
的方程;
(2)設點![]() ,直線
,直線![]() 與橢圓
與橢圓![]() 交于另一點
交于另一點![]() ,直線
,直線![]() 與橢圓
與橢圓![]() 交于另一點
交于另一點![]() .設
.設![]() 的斜率為
的斜率為![]() ,則
,則![]() 是否為定值?若是,求出該定值;若不是,請說明理由.
是否為定值?若是,求出該定值;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的焦距為
的焦距為![]() ,橢圓
,橢圓![]() 上任意一點到橢圓兩個焦點的距離之和為6.
上任意一點到橢圓兩個焦點的距離之和為6.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)設直線![]()
![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點,點
兩點,點![]() (0,1),且
(0,1),且![]() =
=![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某生鮮批發店每天從蔬菜生產基地以5元/千克購進某種綠色蔬菜,售價8元/千克,若每天下午4點以前所購進的綠色蔬菜沒有售完,則對未售出的綠色蔬菜降價處理,以3元/千克出售.根據經驗,降價后能夠把剩余蔬菜全部處理完畢,且當天不再進貨.該生鮮批發店整理了過往30天(每天下午4點以前)這種綠色蔬菜的日銷售量(單位:千克)得到如下統計數據(視頻率為概率)(注:x,y∈N*)
每天下午4點前銷售量 | 350 | 400 | 450 | 500 | 550 |
天數 | 3 | 9 | x | y | 2 |
(1)求在未來3天中,至少有1天下午4點前的銷售量不少于450千克的概率.
(2)若該生鮮批發店以當天利潤期望值為決策依據,當購進450千克比購進500千克的利潤期望值大時,求x的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=(x﹣2)ex﹣![]() +
+![]() x,其中
x,其中![]() ∈R,e是自然對數的底數.
∈R,e是自然對數的底數.
(1)當![]() >0時,討論函數f(x)在(1,+∞)上的單調性;
>0時,討論函數f(x)在(1,+∞)上的單調性;
(2)若函數g(x)=f![]() (x)+2﹣
(x)+2﹣![]() ,證明:使g(x)≥0在
,證明:使g(x)≥0在![]() 上恒成立的實數a能取到的最大整數值為1.
上恒成立的實數a能取到的最大整數值為1.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,其圖象關于直線
,其圖象關于直線![]() 對稱,為了得到函數
對稱,為了得到函數![]() 的圖象,只需將函數
的圖象,只需將函數![]() 的圖象上的所有點( )
的圖象上的所有點( )
A.先向左平移![]() 個單位長度,再把所得各點橫坐標伸長為原來的2倍,縱坐標保持不變
個單位長度,再把所得各點橫坐標伸長為原來的2倍,縱坐標保持不變
B.先向右平移![]() 個單位長度,再把所得各點橫坐標縮短為原來的
個單位長度,再把所得各點橫坐標縮短為原來的![]() ,縱坐標保持不變
,縱坐標保持不變
C.先向右平移![]() 個單位長度,再把所得各點橫坐標伸長為原來的2倍,縱坐標保持不變
個單位長度,再把所得各點橫坐標伸長為原來的2倍,縱坐標保持不變
D.先向左平移![]() 個單位長度,再把所得各點橫坐標縮短為原來的
個單位長度,再把所得各點橫坐標縮短為原來的![]() ,縱坐標保持不變
,縱坐標保持不變
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,射線![]() 和
和![]() 均為筆直的公路,扇形
均為筆直的公路,扇形![]() 區域(含邊界)是一蔬菜種植園,其中
區域(含邊界)是一蔬菜種植園,其中![]() 、
、![]() 分別在射線
分別在射線![]() 和
和![]() 上.經測量得,扇形
上.經測量得,扇形![]() 的圓心角(即
的圓心角(即![]() )為
)為![]() 、半徑為1千米.為了方便菜農經營,打算在扇形
、半徑為1千米.為了方便菜農經營,打算在扇形![]() 區域外修建一條公路
區域外修建一條公路![]() ,分別與射線
,分別與射線![]() 、
、![]() 交于
交于![]() 、
、![]() 兩點,并要求
兩點,并要求![]() 與扇形弧
與扇形弧![]() 相切于點
相切于點![]() .設
.設![]() (單位:弧度),假設所有公路的寬度均忽略不計.
(單位:弧度),假設所有公路的寬度均忽略不計.
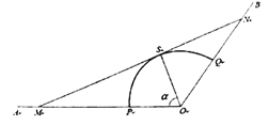
(1)試將公路![]() 的長度表示為
的長度表示為![]() 的函數,并寫出
的函數,并寫出![]() 的取值范圍;
的取值范圍;
(2)試確定![]() 的值,使得公路
的值,使得公路![]() 的長度最小,并求出其最小值.
的長度最小,并求出其最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地擬建造一座體育館,其設計方案側面的外輪廓線如圖所示:曲線![]() 是以點
是以點![]() 為圓心的圓的一部分,其中
為圓心的圓的一部分,其中![]()
![]() ,
,![]() 是圓的切線,且
是圓的切線,且![]() ,曲線
,曲線![]() 是拋物線
是拋物線![]()
![]() 的一部分,
的一部分,![]() ,且
,且![]() 恰好等于圓
恰好等于圓![]() 的半徑.
的半徑.
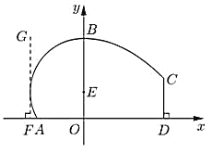
(1)若![]() 米,
米,![]() 米,求
米,求![]() 與
與![]() 的值;
的值;
(2)若體育館側面的最大寬度![]() 不超過75米,求
不超過75米,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com