
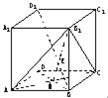
 在棱長為1的正方體ABCD-A1B1C1D1中,BD1交平面ACB1于點E,
在棱長為1的正方體ABCD-A1B1C1D1中,BD1交平面ACB1于點E, ED1.
ED1.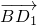 =
= +
+ +
+ ,
, =
= +
+ ,
,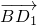 •
• =(
=( +
+ +
+ )•(
)•( +
+ )
) •
• +
+ •
• =
= •
• -
- •
• =|
=| |2-|
|2-| |2
|2 =
=
 =
=
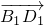 ,即2
,即2 =
=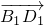 .
. =b,
=b, =m,
=m,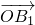 =b1,
=b1,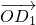 =d1,
=d1,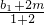 =
=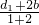 =e.
=e. ED1.
ED1.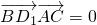 ,
,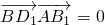 ,從而證明BD1⊥平面ACB1;
,從而證明BD1⊥平面ACB1; =
=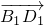 .設(shè)
.設(shè) =b,
=b, =m,
=m,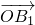 =b1,
=b1,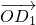 =d1,求得點E分線段B1M及D1B各成λ(λ=2)之比,點E是D1B與平面ACB1之交點,此交點E將D1B分成2與1之比,即BE=
=d1,求得點E分線段B1M及D1B各成λ(λ=2)之比,點E是D1B與平面ACB1之交點,此交點E將D1B分成2與1之比,即BE= ED1.
ED1.

 世紀(jì)百通期末金卷系列答案
世紀(jì)百通期末金卷系列答案科目:高中數(shù)學(xué) 來源: 題型:
 在線段AD1上運動,給出以下四個命題:
在線段AD1上運動,給出以下四個命題:查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
 (理科)如圖,在棱長為1的正方體A'C中,過BD及B'C'的中點E作截面BEFD交C'D'于F.
(理科)如圖,在棱長為1的正方體A'C中,過BD及B'C'的中點E作截面BEFD交C'D'于F.查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
 (2004•武漢模擬)(文科)在棱長為1的正方體ABCD-A′B′C′D′中,AC′為對角線,M、N分別為BB′,B′C′中點,P為線段MN中點.
(2004•武漢模擬)(文科)在棱長為1的正方體ABCD-A′B′C′D′中,AC′為對角線,M、N分別為BB′,B′C′中點,P為線段MN中點.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com