
【題目】如圖,在三棱柱![]() 中,
中,![]() 平面
平面![]() 為正三角形, 側面
為正三角形, 側面![]() 是邊長為
是邊長為![]() 的正方形,
的正方形,![]() 為
為![]() 的中點.
的中點.
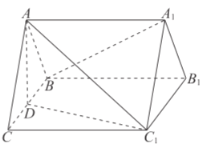
(1)求證![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)試判斷直線![]() 與平面
與平面![]() 的位置關系,并加以證明.
的位置關系,并加以證明.
【答案】(1)證明見解析(2)![]() (3)直線
(3)直線![]() 與平面
與平面![]() 相交.證明見解析
相交.證明見解析
【解析】
(1)根據線面平行的判定定理,在面![]() 內找一條直線平行于
內找一條直線平行于![]() 即可.所以連接
即可.所以連接![]() 交
交![]() 與點
與點![]() ,再連接
,再連接![]() ,由中位線定理可得
,由中位線定理可得![]() ,即可得證;
,即可得證;
(2)取![]() 的中點
的中點![]() ,連接
,連接![]() .分別以
.分別以![]() ,
,![]() ,
,![]() 為
為![]() 軸,
軸,![]() 軸,
軸,![]() 軸,如圖建立空間直角坐標系,再根據二面角的向量方法即可求出;
軸,如圖建立空間直角坐標系,再根據二面角的向量方法即可求出;
(3)根據平面![]() 的法向量與直線
的法向量與直線![]() 的方向向量的關系,即可判斷直線
的方向向量的關系,即可判斷直線![]() 與平面
與平面![]() 的位置關系.
的位置關系.
(1)由題意,三棱柱![]() 為正三棱柱.
為正三棱柱.
連接![]() . 設
. 設![]() ,則
,則![]() 是
是![]() 的中點.連接
的中點.連接![]() , 由
, 由![]() ,
,![]() 分別為
分別為![]() 和
和![]() 的中點,得
的中點,得![]() .又因為
.又因為![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
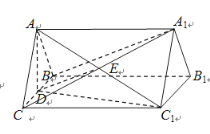
(2)取![]() 的中點
的中點![]() ,連接
,連接![]() .
.
因為![]()
![]() 為正三角形,且
為正三角形,且![]() 為
為![]() 中點,所以
中點,所以![]() .
.
由![]() ,
,![]() 分別為
分別為![]() 和
和![]() 的中點,得
的中點,得![]() ,
,
又因為![]() 平面
平面![]() , 所以
, 所以![]() 平面
平面![]() ,即有
,即有![]() ,
,![]() .
.
分別以![]() ,
,![]() ,
,![]() 為
為![]() 軸,
軸,![]() 軸,
軸,![]() 軸,如圖建立空間直角坐標系,
軸,如圖建立空間直角坐標系,
則![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,![]() ,
,
設平面![]() 的法向量
的法向量![]() ,
,
由![]() ,
,![]() ,得
,得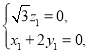
令![]() ,得
,得![]() .
.
設平面![]() 的法向量
的法向量![]() ,
,
由![]() ,
,![]() ,得
,得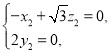
令![]() ,得
,得![]() .
.
設二面角![]() 的平面角為
的平面角為![]() ,則
,則 ![]() .
.
由圖可得二面角![]() 為銳二面角,
為銳二面角,
所以二面角![]() 的余弦值為
的余弦值為![]() .
.

(3)結論:直線![]() 與平面
與平面![]() 相交.
相交.
證明:因為![]() ,
,![]() ,且
,且![]() ,
,
所以![]() .
.
又因為平面![]() 的法向量
的法向量![]() ,且
,且![]() ,
,
所以![]() 與
與![]() 不垂直,
不垂直,
因為![]() 平面
平面![]() ,且
,且![]() 與平面
與平面![]() 不平行,
不平行,
故直線![]() 與平面
與平面![]() 相交.
相交.


 出彩同步大試卷系列答案
出彩同步大試卷系列答案科目:高中數學 來源: 題型:
【題目】某公司為了了解年研發資金投人量![]() (單位:億元)對年銷售額
(單位:億元)對年銷售額![]() (單位:億元)的影響.對公司近
(單位:億元)的影響.對公司近![]() 年的年研發資金投入量
年的年研發資金投入量![]() 和年銷售額
和年銷售額![]() 的數據,進行了對比分析,建立了兩個函數模型:①
的數據,進行了對比分析,建立了兩個函數模型:①![]() ,②
,②![]() ,其中
,其中![]() 、
、![]() 、
、![]() 、
、![]() 均為常數,
均為常數,![]() 為自然對數的底數.并得到一些統計量的值.令
為自然對數的底數.并得到一些統計量的值.令![]() ,
,![]() ,經計算得如下數據:
,經計算得如下數據:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)請從相關系數的角度,分析哪一個模型擬合程度更好?
(2)(ⅰ)根據(1)的選擇及表中數據,建立![]() 關于
關于![]() 的回歸方程;
的回歸方程;
(ⅱ)若下一年銷售額![]() 需達到
需達到![]() 億元,預測下一年的研發資金投入量
億元,預測下一年的研發資金投入量![]() 是多少億元?
是多少億元?
附:①相關系數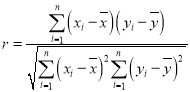 ,
,
回歸直線![]() 中公式分別為:
中公式分別為: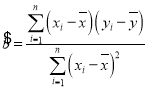 ,
,![]() ;
;
②參考數據:![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的長軸是短軸的兩倍,以短軸一個頂點和長軸一個頂點為端點的線段作直徑的圓的周長等于
的長軸是短軸的兩倍,以短軸一個頂點和長軸一個頂點為端點的線段作直徑的圓的周長等于![]() ,直線l與橢圓C交于
,直線l與橢圓C交于![]() 兩點.
兩點.
(1)求橢圓C的方程;
(2)過點O作直線l的垂線,垂足為D.若![]() ,求動點D的軌跡方程.
,求動點D的軌跡方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 為平面內一定點,動點
為平面內一定點,動點![]() 為平面內曲線
為平面內曲線![]() 上的任意一點,且滿足
上的任意一點,且滿足![]() ,過原點的直線交曲線
,過原點的直線交曲線![]() 于
于![]() 兩點.
兩點.
(1)證明:直線![]() 與直線
與直線![]() 的斜率之積為定值;
的斜率之積為定值;
(2)設直線![]() ,
,![]() 交直線
交直線![]() 于
于![]() 、
、![]() 兩點,求線段
兩點,求線段![]() 長度的最小值.
長度的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是2017年第一季度五省GDP情況圖,則下列陳述中不正確的是( )
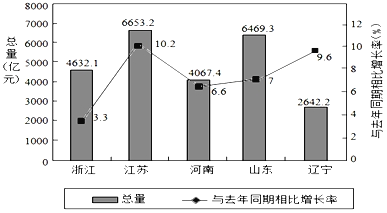
A.2017年第一季度GDP增速由高到低排位第5的是浙江省.
B.與去年同期相比,2017年第一季度的GDP總量實現了增長.
C.2017年第一季度GDP總量和增速由高到低排位均居同一位的省只有1個
D.去年同期河南省的GDP總量不超過4000億元.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() ,
,![]() 滿足
滿足![]() (
(![]() …).
…).
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() 且
且![]() ,則數列
,則數列![]() 中第幾項最小?請說明理由;
中第幾項最小?請說明理由;
(3)若![]() (n=1,2,3,…),求證:“數列
(n=1,2,3,…),求證:“數列![]() 為等差數列”的充分必要條件是“數列
為等差數列”的充分必要條件是“數列![]() 為等差數列且
為等差數列且![]() (n=1,2,3,…)”.
(n=1,2,3,…)”.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于定義域為![]() 的函數
的函數![]() ,如果存在區間
,如果存在區間![]() ,其中
,其中![]() ,同時滿足:
,同時滿足:
①![]() 在
在![]() 內是單調函數:②當定義域為
內是單調函數:②當定義域為![]() 時,
時,![]() 的值域為
的值域為![]() ,則稱函數
,則稱函數![]() 是區間
是區間![]() 上的“保值函數”,區間
上的“保值函數”,區間![]() 稱為“保值函數”.
稱為“保值函數”.
(1)求證:函數![]() 不是定義域
不是定義域![]() 上的“保值函數”;
上的“保值函數”;
(2)若函數![]() (
(![]() )是區間
)是區間![]() 上的“保值函數”,求
上的“保值函數”,求![]() 的取值范圍;
的取值范圍;
(3)對(2)中函數![]() ,若不等式
,若不等式![]() 對
對![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線C的參數方程為
中,曲線C的參數方程為![]() (
(![]() 為參數).以坐標原點O為極,z軸正半軸為極軸建立極坐標系,直線
為參數).以坐標原點O為極,z軸正半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ)求曲線C的普通方程和直線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)設點![]() .若直線
.若直線![]() 與曲線C相交于A,B兩點,求
與曲線C相交于A,B兩點,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com