
【題目】在平面直角坐標系![]() 中,曲線C的參數方程為
中,曲線C的參數方程為![]() (
(![]() 為參數).以坐標原點O為極,z軸正半軸為極軸建立極坐標系,直線
為參數).以坐標原點O為極,z軸正半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ)求曲線C的普通方程和直線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)設點![]() .若直線
.若直線![]() 與曲線C相交于A,B兩點,求
與曲線C相交于A,B兩點,求![]() 的值.
的值.
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱![]() 中,
中,![]() 平面
平面![]() 為正三角形, 側面
為正三角形, 側面![]() 是邊長為
是邊長為![]() 的正方形,
的正方形,![]() 為
為![]() 的中點.
的中點.
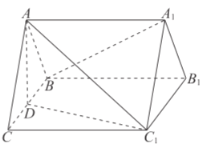
(1)求證![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)試判斷直線![]() 與平面
與平面![]() 的位置關系,并加以證明.
的位置關系,并加以證明.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】空氣質量指數![]() 是反映空氣質量狀況的指數,
是反映空氣質量狀況的指數,![]() 指數值越小,表明空氣質量越好,其對應關系如表:
指數值越小,表明空氣質量越好,其對應關系如表:
|
|
|
|
|
|
|
空氣質量 | 優 | 良 | 輕度污染 | 中度污染 | 重度污染 | 嚴重污染 |
如圖是某市10月1日—20日![]() 指數變化趨勢:
指數變化趨勢:
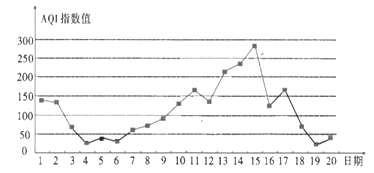
下列敘述正確的是( )
A.該市10月的前半個月的空氣質量越來越好
B.這20天中的中度污染及以上的天數占![]()
C.這20天中![]() 指數值的中位數略高于100
指數值的中位數略高于100
D.總體來說,該市10月上旬的空氣質量比中旬的空氣質量差
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某高新企業自2012年成立以來,不斷創新技術與產品,積極拓展市場,銷售收入![]() (單位萬元)與年份代號
(單位萬元)與年份代號![]() 之間對應關系如下表,且滿足回歸函數
之間對應關系如下表,且滿足回歸函數![]() ,記
,記![]() 。
。
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
銷售收入 | 80 | 199 | 398 | 2512 | 6310 | 15848 | 79432 |
| 1.9 | 2.3 | 2.6 | 3.4 | 3.8 | 4.2 | 4.9 |
(1)任取2年對比銷售收入的情況,求這2年中銷售收入均超過400萬元的概率;
(2)求回歸函數![]() 中
中![]() 的值。
的值。
附:對于一組數據![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為
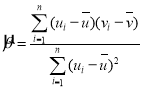 ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某健康社團為調查居民的運動情況,統計了某小區100名居民平均每天的運動時長(單位:小時)并根據統計數據分為![]() 六個小組(所調查的居民平均每天運動時長均在
六個小組(所調查的居民平均每天運動時長均在![]() 內),得到的頻率分布直方圖如圖所示.
內),得到的頻率分布直方圖如圖所示.
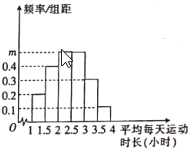
(1)求出圖中![]() 的值,并估計這
的值,并估計這![]() 名居民平均每天運動時長的平均值及中位數(同一組中的每個數據可用該組區間的中點值代替);
名居民平均每天運動時長的平均值及中位數(同一組中的每個數據可用該組區間的中點值代替);
(2)為了分析出該小區居民平均每天的運動量與職業、年齡等的關系,該社團按小組用分層抽樣的方法抽出20名居民進一步調查,試問在![]() 時間段內應抽出多少人?
時間段內應抽出多少人?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一幢高樓上安放了一塊高約10 米的 LED 廣告屏,一測量愛好者在與高樓底部同一水平線上的 C 處測得廣告屏頂端A 處的仰角為 31.80°,再向大樓前進 20 米到 D 處,測得廣告屏頂端 A 處的仰角為 37.38°(人的高度忽略不計).
(1)求大樓的高度(從地面到廣告屏頂端)(精確到 1 米);
(2)若大樓的前方是一片公園空地,空地上可以安放一些長椅,為使坐在其中一個長椅上觀看廣告屏最清晰(長 椅的高度忽略不計),長椅需安置在距大樓底部 E 處多遠?已知視角 ∠AMB( M 為觀測者的位置, B 為廣告屏 底部)越大,觀看得越清晰.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,三棱柱![]() 中,
中,![]() 側面
側面![]() ,已知
,已知![]() ,
,![]() ,
,![]() ,點
,點![]() 是棱
是棱![]() 的中點.
的中點.
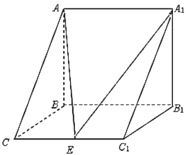
(1)求證:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)在棱![]() 上是否存在一點
上是否存在一點![]() ,使得
,使得![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com