【題目】已知橢圓C：
的離心率為
，短軸長為4.
（1）求橢圓C的標準方程；
（2）已知不經過點P（0，2）的直線l：
交橢圓C于A，B兩點，M在AB上滿足
且
，問直線是否過定點，若過求定點坐標；若不過，請說明理由。
【答案】（1）
（2）直線
恒過定點
，詳見解析
【解析】
（1）根據題意可得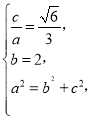
，解出方程可得橢圓
的標準方程；（2）設
，
，根據向量的關系以及三角形的性質可得
為
外接圓的直徑，即
，根據點A，B在直線上可得
，聯立直線與橢圓的方程，運用韋達定理代入可得
，解出方程
或
，代入直線中即可得定點.
解：（1）由題意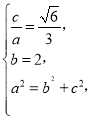得解得
，
，
所以橢圓的標準方程為．
（2）設，，
又
，所以
，
，
因為
在上滿足
，所以為的中點．
又
，即
，
所以線段為外接圓的直徑，
即，
所以
．
又
在直線上，
所以
，
即，
聯立
消
得
，
因為直線與橢圓交于不同的兩點，
所以
，
即
，
由韋達定理得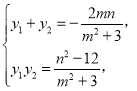
代入（*）中，得，
解得或，
所以直線：
或
，
所以直線過定點或
（舍去），
綜上所述：直線恒過定點．
黃岡天天練口算題卡系列答案科目：高中數學 來源： 題型：
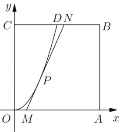
【題目】某地要建造一個邊長為2（單位：
）的正方形市民休閑公園
，將其中的區域
開挖成一個池塘，如圖建立平面直角坐標系后，點
的坐標為
，曲線
是函數
圖像的一部分，過邊
上一點
在區域
內作一次函數
（
）的圖像，與線段
交于點
（點不與點重合），且線段
與曲線有且只有一個公共點
，四邊形
為綠化風景區.
（1）求證：
；
（2）設點的橫坐標為
，
①用表示、兩點的坐標；
②將四邊形的面積
表示成關于的函數
，并求的最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某高校大一新生中,來自東部地區的學生有2400人、中部地區學生有1600人、西部地區學生有1000人.從中選取100人作樣本調研飲食習慣,為保證調研結果相對準確,下列判斷正確的有（ ）
①用分層抽樣的方法分別抽取東部地區學生48人、中部地區學生32人、西部地區學生20人；
②用簡單隨機抽樣的方法從新生中選出100人；
③西部地區學生小劉被選中的概率為
；
④中部地區學生小張被選中的概率為
A. ①④ B. ①③ C. ②④ D. ②③
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某企業為了檢查生產
產品的甲、乙兩條流水線的生產情況，隨機地從這兩條流水線上生產的大量產品中各抽取50件產品作為樣本，測出它們的這一項質量指標值.若該項質量指標值落在
內，則為合格品，否則為不合格品.下表是甲流水線樣本的頻數分布表，下圖是乙流水線樣本的頻率分布直方圖.
甲流水線樣本的頻數分布表
質量指標值 | 頻數 |
| 9 |
| 10 |
| 17 |
| 8 |
| 6 |
乙流水線樣本的頻率分布直方圖
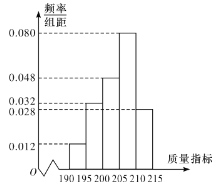
（1）根據圖形，估計乙流水線生產的產品的該項質量指標值的中位數；
（2）設該企業生產一件合格品獲利100元，生產一件不合格品虧損50元，若某個月內甲、乙兩條流水線均生產了1000件產品，若將頻率視為概率，則該企業本月的利潤約為多少元？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐
中，
平面ABCD，底部ABCD為菱形，E為CD的中點.
（Ⅰ）求證：BD⊥平面PAC；
（Ⅱ）若∠ABC=60°，求證：平面PAB⊥平面PAE；
（Ⅲ）棱PB上是否存在點F，使得CF∥平面PAE？說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
