Question

17．已知O為△ABC的外心，且$cosA=\frac{1}{3}$，若$\overrightarrow{AO}=α\overrightarrow{AB}+β\overrightarrow{AC}$，則α+β的最大值為$\frac{3}{4}$．

Answer 1

分析 用$\overrightarrow{OB}，\overrightarrow{OC}$表示出$\overrightarrow{OA}$，兩邊平方，利用2倍角公式得出α+β與αβ的關系，再利用基本不等式得出α+β的范圍．

解答 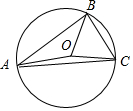解：∵$\overrightarrow{AO}=α\overrightarrow{AB}+β\overrightarrow{AC}$，
∴-$\overrightarrow{OA}$=α（$\overrightarrow{OB}-\overrightarrow{OA}$）+β（$\overrightarrow{OC}$-$\overrightarrow{OA}$），
∴（α+β-1）$\overrightarrow{OA}$=α$\overrightarrow{OB}$+β$\overrightarrow{OC}$，
∴α+β-1＜0，即α+β＜1．
∵cosA=$\frac{1}{3}$，∴cos∠BOC=cos2A=2cos²A-1=-$\frac{7}{9}$，
設△ABC的外接圓半徑為R，則（α+β-1）²R²=α²R²+β²R²-$\frac{14}{9}$αβR²，
整理得：18（α+β）=9+32αβ，
∵αβ≤（$\frac{α+β}{2}$）²，
∴18（α+β）≤9+32•$\frac{（α+β）^{2}}{4}$，解得α+β≤$\frac{3}{4}$或α+β≥$\frac{3}{2}$（舍），
故答案為：$\frac{3}{4}$．

點評 本題考查了平面向量的基本定理，平面向量的數量積運算，借助幾何關系得出平面向量的關系是解題關鍵，屬于中檔題．