拋物線y2=4x上有兩個定點A、B分別在對稱軸的上、下兩側,F為拋物線的焦點,并且|FA|=2,|FB|=5,在拋物線AOB這段曲線上求一點P,使△PAB的面積最大,并求這個最大面積.
【答案】
分析:由已知得F(1,0),點A在x軸上方,設A(x
1,y
1),y
1>0,由|FA|=2得A(1,2),同理B(4,-4),所以直線AB的方程為2x+y-4=0.設在拋物線AOB這段曲線上任一點P(x
,y
),且0≤x
≤4,-4≤y
≤2,由點到直線距離公式能求出△PAB的面積最大值和此時P點坐標.
解答:解:由已知得F(1,0),點A在x軸上方,
設A(x
1,y
1),y
1>0,
由|FA|=2,
得x
1+1=2,x
1=1,
所以A(1,2),
同理B(4,-4),
所以直線AB的方程為2x+y-4=0.
設在拋物線AOB這段曲線上任一點P(x
,y
),
且0≤x
≤4,-4≤y
≤2.
則點P到直線AB的距離d=
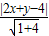
=
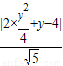
=
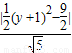
,
所以當y
=-1時,d取最大值
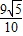
,
又|AB|=3
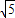
,
所以△PAB的面積最大值為
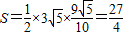
.
此時P點坐標為(

,-1).
點評:本題主要考查拋物線標準方程,簡單幾何性質,直線與拋物線的位置關系等基礎知識.考查運算求解能力,推理論證能力;考查化歸與轉化思想.解題時要認真審題,注意點到直線距離公式的合理運用.

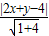 =
=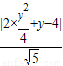 =
=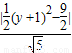 ,
,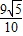 ,
,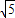 ,
,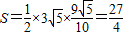 .
. ,-1).
,-1).

 每日10分鐘口算心算速算天天練系列答案
每日10分鐘口算心算速算天天練系列答案