
【題目】已知橢圓的一個頂點為A(0,-1),焦點在x軸上。若右焦點F到直線x-y+2![]() =0的距離為3。
=0的距離為3。
(1)求橢圓的方程;
(2)設直線y=kx+m(k≠0)與橢圓相交于不同的兩點M、N。當|AM|=|AN|時,求m的取值范圍。
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】試題分析:(1)根據右焦點到直線x﹣y+![]() =0的距離為3,利用點到直線的距離公式求出c,再由橢圓的一個頂點為A(0,﹣1),求出b,從而得到橢圓方程.(2)設A為弦MN的中點,由
=0的距離為3,利用點到直線的距離公式求出c,再由橢圓的一個頂點為A(0,﹣1),求出b,從而得到橢圓方程.(2)設A為弦MN的中點,由 ,得(3k2+1)x2+6kmx+3(m2﹣1)=0.利用根的判別式和韋達定理,結合題設能求出m的取值范圍.
,得(3k2+1)x2+6kmx+3(m2﹣1)=0.利用根的判別式和韋達定理,結合題設能求出m的取值范圍.
解析:
(1) 設右焦點F(c,0),(c>0),則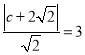 ,∴
,∴![]() .∵橢圓的一個頂點為A(0,﹣1),∴b=1,a2=3,∴橢圓方程是
.∵橢圓的一個頂點為A(0,﹣1),∴b=1,a2=3,∴橢圓方程是![]() .
.
(2)設P為弦MN的中點,由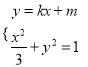 得(3k2+1)x2+6kmx+3(m2﹣1)=0.
得(3k2+1)x2+6kmx+3(m2﹣1)=0.
由△>0,得m2<3k2+1 ①,
∴xP=![]() ,
,
從而yP=kxp+m=![]() .
.
∴kBP=![]() .
.
由MN⊥AP,得![]() =﹣
=﹣![]() ,
,
即2m=3k2+1②.
將②代入①,得2m>m2,
解得0<m<2.由②得k2=![]() >0.
>0.
解得m>![]() .故所求m的取值范圍為(
.故所求m的取值范圍為(![]() ,2).
,2).


 名校名師培優作業本加核心試卷系列答案
名校名師培優作業本加核心試卷系列答案 全程金卷系列答案
全程金卷系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() (
(![]() >b>0)的左、右頂點分別為A1、A2,上、下頂點分別為B2、B1,O為坐標原點,四邊形A1B1A2B2的面積為4,且該四邊形內切圓的方程為
>b>0)的左、右頂點分別為A1、A2,上、下頂點分別為B2、B1,O為坐標原點,四邊形A1B1A2B2的面積為4,且該四邊形內切圓的方程為![]() .
.
(Ⅰ)求橢圓C的方程;
(Ⅱ)若M、N是橢圓C上的兩個不同的動點,直線OM、ON的斜率之積等于![]() ,試探求△OMN的面積是否為定值,并說明理由.
,試探求△OMN的面積是否為定值,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐P-ABCD中,PA⊥平面ABCD,底面ABCD是邊長為2的正方形,
PA=AD,F為PD的中點.
(1)求證:AF⊥平面PDC;
(2)求直線AC與平面PCD所成角的大小.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]()
(1)證明函數f ( x )的圖象關于![]() 軸對稱;
軸對稱;
(2)判斷![]() 在
在![]() 上的單調性,并用定義加以證明;
上的單調性,并用定義加以證明;
(3)當x∈[1,2]時函數f (x )的最大值為![]() ,求此時a的值。
,求此時a的值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設△ABC的內角A、B、C所對的邊長分別為a、b、c,且acos B=3,bsin A=4.
(1)求邊長a;
(2)若△ABC的面積S=10,求△ABC的周長l.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】遼寧號航母紀念章從2012年10月5日起開始上市,通過市場調查,得到該紀念章每![]() 枚的市場價
枚的市場價![]() (單位:元)與上市時間
(單位:元)與上市時間![]() (單位:天)的數據如下:
(單位:天)的數據如下:
上市時間 |
|
|
|
市場價 |
|
|
|
(1)根據上表數據,從下列函數中選取一個恰當的函數描述遼寧號航母紀念章的市場價![]() 與上市時間
與上市時間![]() 的變化關系:①
的變化關系:①![]() ;②
;②![]() ;③
;③![]() ;
;
(2)利用你選取的函數,求遼寧號航母紀念章市場價最低時的上市天數及最低的價格;
(3)設你選取的函數為![]() ,若對任意實數
,若對任意實數![]() ,關于
,關于![]() 的方程
的方程![]() 恒有個想異實數根,求
恒有個想異實數根,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com