解:(1)由S
n=S
n-1+a
n-1+

,得S
n-S
n-1=a
n-1+

,2a
n=2a
n-1+1,a
n-a
n-1+

…2分
∴a
n=a
1+(n-1)d=

n-

(2)證明:∵3b
n-b
n-1=n,∴b
n=

b
n-1+

n,
∴b
n-a
n=

b
n-1+

n-

n+

=

b
n-1-

n+

=

(b
n-1-

n+

);
b
n-1-a
n-1=b
n-1-

(n-1)+

=b
n-1-

n+

;
∴由上面兩式得
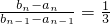
,又b
1-a
1=-
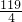
-

=-30
∴數列{b
n-a
n}是以-30為首項,

為公比的等比數列.
(3)由(2)得b
n-a
n=-30×

,
∴
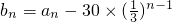
=
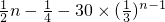
,
b
n-b
n-1=
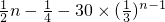
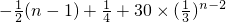
=
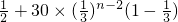
=
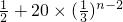
>0,∴{b
n}是遞增數列
當n=1時,b
1=-
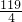
<0;當n=2時,b
2=
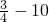
<0;
當n=3時,b
3=
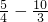
<0;當n=4時,b
4=
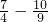
>0,
所以,從第4項起的各項均大于0,故前3項之和最小.
且S
3=
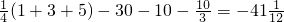
.
分析:(1)利用S
n-S
n-1=a
n,直接求出{a
n}的通項公式;
(2)直接求出數列b
n-a
n表達式,利用等比數列的定義證明數列{b
n-a
n}為等比數列;
(3)利用(2)求出數列的前幾項,即可判斷數列的符號,然后求{b
n}前n項和的最小值.
點評:本題是中檔題,考查數列的遞推關系式的應用,考查邏輯推理能力,計算能力,轉化思想的應用.

 且Sn=Sn-1+an-1+
且Sn=Sn-1+an-1+ ,數列{bn}滿足b1=-
,數列{bn}滿足b1=-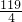 且3bn-bn-1=n(n≥2且n∈N*).
且3bn-bn-1=n(n≥2且n∈N*). ,得Sn-Sn-1=an-1+
,得Sn-Sn-1=an-1+ ,2an=2a n-1+1,an-a n-1+
,2an=2a n-1+1,an-a n-1+ …2分
…2分 n-
n-
 bn-1+
bn-1+ n,
n, bn-1+
bn-1+ n-
n- n+
n+ =
= bn-1-
bn-1- n+
n+ =
= (bn-1-
(bn-1- n+
n+ );
); (n-1)+
(n-1)+ =bn-1-
=bn-1- n+
n+ ;
;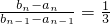 ,又b1-a1=-
,又b1-a1=-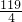 -
- =-30
=-30 為公比的等比數列.
為公比的等比數列. ,
,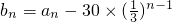 =
=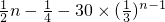 ,
,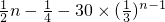
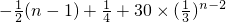
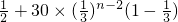
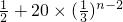 >0,∴{bn}是遞增數列
>0,∴{bn}是遞增數列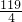 <0;當n=2時,b2=
<0;當n=2時,b2=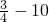 <0;
<0;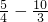 <0;當n=4時,b4=
<0;當n=4時,b4=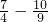 >0,
>0,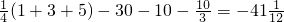 .
.
