
【題目】在下列命題中,正確的命題有________(填寫正確的序號(hào))
①若![]() ,則
,則![]() 的最小值是6;
的最小值是6;
②如果不等式![]() 的解集是
的解集是![]() ,那么
,那么![]() 恒成立;
恒成立;
③設(shè)x,![]() ,且
,且![]() ,則
,則![]() 的最小值是
的最小值是![]() ;
;
④對(duì)于任意![]() ,
,![]() 恒成立,則t的取值范圍是
恒成立,則t的取值范圍是![]() ;
;
⑤“![]() ”是“復(fù)數(shù)
”是“復(fù)數(shù)![]() (
(![]() )是純虛數(shù)”的必要非充分條件;
)是純虛數(shù)”的必要非充分條件;
⑥若![]() ,
,![]() ,
,![]() ,則必有
,則必有![]() ;
;
【答案】①②③④⑥
【解析】
①![]() ,利用均值定理求最值即可;
,利用均值定理求最值即可;
②由一元二次不等式與一元二次方程的關(guān)系,利用韋達(dá)定理求解即可;
③由![]() 得
得![]() ,代入式子中可得關(guān)于
,代入式子中可得關(guān)于![]() 的函數(shù),進(jìn)而求得最值即可;
的函數(shù),進(jìn)而求得最值即可;
④設(shè)![]() ,則可轉(zhuǎn)化為在
,則可轉(zhuǎn)化為在![]() 時(shí),
時(shí),![]() ,進(jìn)而求解即可;
,進(jìn)而求解即可;
⑤由純虛數(shù)的定義可知虛部不為0,實(shí)部為0,進(jìn)而判斷即可;
⑥由![]() 可得
可得![]() ,代入
,代入![]() 中可得
中可得![]() ,再將
,再將![]() 代入
代入![]() 求解即可
求解即可
①因?yàn)?/span>![]() ,所以
,所以![]() ,所以
,所以![]() ,當(dāng)且僅當(dāng)
,當(dāng)且僅當(dāng)![]() ,即
,即![]() 時(shí),等號(hào)成立,故①正確;
時(shí),等號(hào)成立,故①正確;
②由不等式與方程的關(guān)系可知![]() 和
和![]() 是方程
是方程![]() 的解,所以
的解,所以![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,則
,則![]() ,故②正確;
,故②正確;
③因?yàn)?/span>![]() ,所以
,所以![]() ,
,
則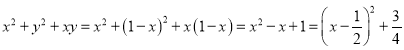 ,
,
則當(dāng)![]() 時(shí),
時(shí),![]() 的最小值為
的最小值為![]() ,故③正確;
,故③正確;
④由題,因?yàn)?/span>![]() ,即
,即![]() 在
在![]() 時(shí)恒成立,
時(shí)恒成立,
當(dāng)![]() 時(shí),
時(shí),![]() ,不成立;
,不成立;
當(dāng)![]() 時(shí),設(shè)
時(shí),設(shè)![]() ,
,
當(dāng)![]() 時(shí),
時(shí),![]() ,解得
,解得![]() 或
或![]() ,所以
,所以![]() ;
;
當(dāng)![]() 時(shí),
時(shí),![]() ,解得
,解得![]() 或
或![]() ,所以
,所以![]() ,
,
綜上,![]() ,故④正確;
,故④正確;
⑤因?yàn)?/span>![]() (
(![]() )是純虛數(shù),所以
)是純虛數(shù),所以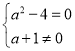 ,解得
,解得![]() 或
或![]() ,
,
所以“![]() ”是“復(fù)數(shù)
”是“復(fù)數(shù)![]() (
(![]() )是純虛數(shù)”的充分不必要條件,故⑤錯(cuò)誤;
)是純虛數(shù)”的充分不必要條件,故⑤錯(cuò)誤;
⑥因?yàn)?/span>![]() ,
,![]() ,所以
,所以![]() ,代入
,代入![]() 可得
可得![]() ,
,
則![]() ,即
,即![]() ,所以
,所以![]() ,
,
即![]() ,
,
所以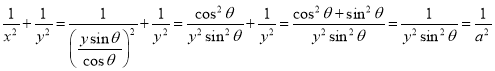 ,
,
故⑥正確;
故答案為: ①②③④⑥



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知正項(xiàng)數(shù)列![]() ,
,![]() 滿足:對(duì)任意正整數(shù)
滿足:對(duì)任意正整數(shù)![]() ,都有
,都有![]() ,
,![]() ,
,![]() 成等差數(shù)列,
成等差數(shù)列,![]() ,
,![]() ,
,![]() 成等比數(shù)列,且
成等比數(shù)列,且![]() ,
,![]() .
.
(Ⅰ)求證:數(shù)列![]() 是等差數(shù)列;
是等差數(shù)列;
(Ⅱ)求數(shù)列![]() ,
,![]() 的通項(xiàng)公式;
的通項(xiàng)公式;
(Ⅲ)設(shè)![]() =
=![]() +
+![]() +…+
+…+![]() ,如果對(duì)任意的正整數(shù)
,如果對(duì)任意的正整數(shù)![]() ,不等式
,不等式![]() 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知點(diǎn)![]() 在
在![]() 上,以R為切點(diǎn)的D的切線的斜率為
上,以R為切點(diǎn)的D的切線的斜率為![]() ,過
,過![]() 外一點(diǎn)A(不在x軸上)作
外一點(diǎn)A(不在x軸上)作![]() 的切線
的切線![]()
![]() ,點(diǎn)BC為切點(diǎn),作平行于
,點(diǎn)BC為切點(diǎn),作平行于![]() 的切線
的切線![]() (切點(diǎn)為D),點(diǎn)MN分別是與
(切點(diǎn)為D),點(diǎn)MN分別是與![]()
![]() 的交點(diǎn)(如圖).
的交點(diǎn)(如圖).
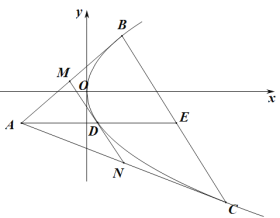
(1)用BC的縱坐標(biāo)st表示直線![]() 的斜率;
的斜率;
(2)設(shè)三角形![]() 面積為S,若將由過
面積為S,若將由過![]() 外一點(diǎn)的兩條切線及第三條切線(平行于兩切線切點(diǎn)的連線)圍成的三角形叫做“切線三角形”,如
外一點(diǎn)的兩條切線及第三條切線(平行于兩切線切點(diǎn)的連線)圍成的三角形叫做“切線三角形”,如![]() ,再由MN作“切線三角形”,并依這樣的方法不斷作切線三角形…,試?yán)?/span>“切線三角形”的面積和計(jì)算由拋物線及
,再由MN作“切線三角形”,并依這樣的方法不斷作切線三角形…,試?yán)?/span>“切線三角形”的面積和計(jì)算由拋物線及![]() 所圍成的陰影部分的面積T.
所圍成的陰影部分的面積T.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在三棱錐P-ABC中,![]() ,平面
,平面![]() 平面ABC,點(diǎn)D在線段BC上,且
平面ABC,點(diǎn)D在線段BC上,且![]() ,E,F分別為線段PC,AB的中點(diǎn),點(diǎn)G是PD上的動(dòng)點(diǎn).
,E,F分別為線段PC,AB的中點(diǎn),點(diǎn)G是PD上的動(dòng)點(diǎn).
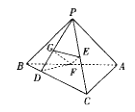
(1)證明:![]() .
.
(2)當(dāng)![]() 平面PAC時(shí),求直線PA與平面EFG所成角的正弦值.
平面PAC時(shí),求直線PA與平面EFG所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 經(jīng)過點(diǎn)
經(jīng)過點(diǎn)![]() 離心率
離心率![]() .
.
(Ⅰ)求橢圓的方程;
(Ⅱ)經(jīng)過橢圓左焦點(diǎn)![]() 的直線(不經(jīng)過點(diǎn)
的直線(不經(jīng)過點(diǎn)![]() 且不與
且不與![]() 軸重合)與橢圓交于
軸重合)與橢圓交于![]() 兩點(diǎn),與直線
兩點(diǎn),與直線![]() :
:![]() 交于點(diǎn)
交于點(diǎn)![]() ,記直線
,記直線![]() 的斜率分別為
的斜率分別為![]() .則是否存在常數(shù)
.則是否存在常數(shù)![]() ,使得向量
,使得向量![]()
![]() 共線?若存在求出
共線?若存在求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓的焦點(diǎn)在x軸上,一個(gè)頂點(diǎn)為![]() ,離心率為
,離心率為![]() ,過橢圓的右焦點(diǎn)F的直線l與坐標(biāo)軸不垂直,且交橢圓于A,B兩點(diǎn).
,過橢圓的右焦點(diǎn)F的直線l與坐標(biāo)軸不垂直,且交橢圓于A,B兩點(diǎn).
![]() 求橢圓的方程;
求橢圓的方程;
![]() 設(shè)點(diǎn)C是點(diǎn)A關(guān)于x軸的對(duì)稱點(diǎn),在x軸上是否存在一個(gè)定點(diǎn)N,使得C,B,N三點(diǎn)共線?若存在,求出定點(diǎn)的坐標(biāo);若不存在,說明理由;
設(shè)點(diǎn)C是點(diǎn)A關(guān)于x軸的對(duì)稱點(diǎn),在x軸上是否存在一個(gè)定點(diǎn)N,使得C,B,N三點(diǎn)共線?若存在,求出定點(diǎn)的坐標(biāo);若不存在,說明理由;
![]() 設(shè)
設(shè)![]() ,是線段
,是線段![]() 為坐標(biāo)原點(diǎn)
為坐標(biāo)原點(diǎn)![]() 上的一個(gè)動(dòng)點(diǎn),且
上的一個(gè)動(dòng)點(diǎn),且![]() ,求m的取值范圍.
,求m的取值范圍.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
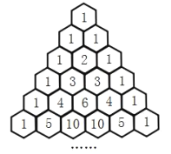
【題目】“楊輝三角”是我國(guó)數(shù)學(xué)史上的一個(gè)偉大成就,是二項(xiàng)式系數(shù)在三角形中的一種幾何排列.如圖所示,第![]() 行的數(shù)字之和為______;去除所有為1的項(xiàng),依此構(gòu)成數(shù)列2,3,3,4,6,4,5,10,10,5,則此數(shù)列的前46項(xiàng)和為______.
行的數(shù)字之和為______;去除所有為1的項(xiàng),依此構(gòu)成數(shù)列2,3,3,4,6,4,5,10,10,5,則此數(shù)列的前46項(xiàng)和為______.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】平行四邊形![]() 所在的平面與直角梯形
所在的平面與直角梯形![]() 所在的平面垂直,
所在的平面垂直,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,![]() 為
為![]() 的中點(diǎn).
的中點(diǎn).
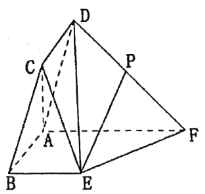
(1)求證:![]() 平面
平面![]() ;
;
(2)求證:![]() ;
;
(3)若直線![]() 上存在點(diǎn)
上存在點(diǎn)![]() ,使得
,使得![]() ,
,![]() 所成角的余弦值為
所成角的余弦值為![]() ,求
,求![]() 與平面
與平面![]() 所成角的大小.
所成角的大小.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】若數(shù)列![]() :
:![]() ,滿足
,滿足![]() ,則稱
,則稱![]() 為
為![]() 數(shù)列,并記
數(shù)列,并記![]() .
.
(1)寫出所有滿足![]() ,
,![]() 的
的![]() 數(shù)列
數(shù)列![]() ;
;
(2)若![]() ,
,![]() ,證明:
,證明:![]() 數(shù)列是遞減數(shù)列的充要條件是
數(shù)列是遞減數(shù)列的充要條件是![]() ;
;
(3)對(duì)任意給定的正整數(shù)![]() ,且
,且![]() ,是否存在
,是否存在![]() 的
的![]() 數(shù)列
數(shù)列![]() ,使得
,使得![]() ?如果存在,求出正整數(shù)
?如果存在,求出正整數(shù)![]() 滿足的條件;如果不存在,說明理由.
滿足的條件;如果不存在,說明理由.
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com