Question

【題目】設f（x）是（﹣∞，+∞）上的奇函數，且f（x+2）=﹣f（x），當0≤x≤1時，f（x）=x．
（1）求f（π）的值；
（2）求﹣1≤x≤3時，f（x）的解析式；
（3）當﹣4≤x≤4時，求f（x）=m（m＜0）的所有實根之和．

Answer 1

【答案】
（1）解：∵f（x+2）=﹣f（x），

∴f（x+4）=﹣f（x+2）=f（x），

即函數f（x）是周期為4的周期函數，

則f（π）=f（π﹣4）=﹣f（4﹣π）=﹣（4﹣π）=π﹣4

（2）解：若﹣1≤x≤0，則0≤﹣x≤1，

則f（﹣x）=﹣x，

∵f（x）是奇函數，∴f（﹣x）=﹣x=﹣f（x），

即f（x）=x，﹣1≤x≤0，

即當﹣1≤x≤1時，f（x）=x，

若1≤x≤3，則﹣1≤x﹣2≤1，

∵f（x+2）=﹣f（x），

∴f（x）=﹣f（x﹣2）=﹣（x﹣2）=﹣x+2，

即當﹣1≤x≤3時，f（x）的解析式為f（x）=

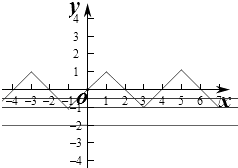
（3）解：作出函數f（x）在﹣4≤x≤4時的圖象如圖，

則函數的最小值為﹣1，

若m＜﹣1，則方程f（x）=m（m＜0）無解，

若m=﹣1，則函數在﹣4≤x≤4上的零點為x=﹣1，x=3，則﹣1+3=2，

若﹣1＜m＜0，則函數在﹣4≤x≤4上共有4個零點，則它們分別關于x=﹣1和x=3對稱，

設分別為a，b，c，d，

則a+b=﹣2，b+d=6，

即a+b+c+d=﹣2+6=4．

【解析】（1）由f（x+2）=﹣f（x），可得f（x+4）=﹣f（x+2）=f（x），即f（x）為周期為4的周期函數，即f（π）=π-4，（2）結合分段函數和函數的奇偶性可得出每段的解析式，（3）作出f（x）在﹣4≤x≤4的圖像，應用數形結合，根據對稱性不難得出所有實根之和為4.
【考點精析】利用函數奇偶性的性質對題目進行判斷即可得到答案，需要熟知在公共定義域內，偶函數的加減乘除仍為偶函數；奇函數的加減仍為奇函數；奇數個奇函數的乘除認為奇函數；偶數個奇函數的乘除為偶函數；一奇一偶的乘積是奇函數;復合函數的奇偶性：一個為偶就為偶，兩個為奇才為奇．