一動圓與兩圓(x+4)2+y2=25和(x-4)2+y2=4都外切,則動圓圓心M的軌跡方程是 .
【答案】
分析:設動圓P的半徑為r,然后根據動圓與圓(x+4)
2+y
2=25,圓(x-4)
2+y
2=1都外切得|MO|=5+r、|MF|=2+r,再兩式相減消去參數r,則滿足雙曲線的定義,找出a與b的值,寫出雙曲線的方程即為動點M的軌跡方程,問題得到解決.
解答:解:設動圓的半徑為r,
由圓(x+4)
2+y
2=25,得到圓心為O(-4,0),半徑為5;
圓(x-4)
2+y
2=4的圓心為F(4,0),半徑為2.
依題意得|MO|=5+r,|MF|=2+r,
則|MO|-|MF|=(5+r)-(2+r)=3<|OF|,
所以點M的軌跡是雙曲線的右支.
∴a=

,c=4,
∴b
2=c
2-a
2=
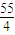
,
則動圓圓心M的軌跡方程是
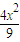
-
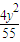
=1(x>0).
故答案為:
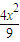
-
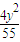
=1(x>0)
點評:本題主要考查雙曲線的定義.本題考查的知識點是圓的方程、橢圓的性質及橢圓與直線的關系,解題的關鍵是根據已知條件中未知圓與已知圓的位置關系,結合“圓的位置關系與半徑及圓心距的關系”,探究出動圓圓心M的軌跡,進而給出動圓圓心M的軌跡方程.

 ,c=4,
,c=4,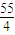 ,
,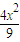 -
-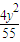 =1(x>0).
=1(x>0).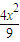 -
-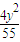 =1(x>0)
=1(x>0)

 閱讀快車系列答案
閱讀快車系列答案