
【題目】已知圓C的極坐標方程為ρ=2cosθ,直線l的參數方程為 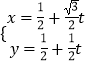 (t為參數),點A的極坐標為(
(t為參數),點A的極坐標為( ![]() ,
, ![]() ),設直線l與圓C交于點P、Q.
),設直線l與圓C交于點P、Q.
(1)寫出圓C的直角坐標方程;
(2)求|AP||AQ|的值.
【答案】
(1)解:圓C的極坐標方程為ρ=2cosθ 即ρ=2ρcosθ,即 (x﹣1)2+y2=1,表示以C(1,0)為圓心、半徑等于1的圓.
(2)解:∵點A的直角坐標為( ![]() ,
, ![]() ),∴點A在直線
),∴點A在直線 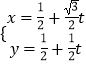 (t為參數)上.
(t為參數)上.
把直線的參數方程代入曲線C的方程可得 t2+ ![]() t﹣
t﹣ ![]() =0.
=0.
由韋達定理可得 t1t2=﹣ ![]() <0,根據參數的幾何意義可得|AP||AQ|=|t1t2|=
<0,根據參數的幾何意義可得|AP||AQ|=|t1t2|= ![]()
【解析】(1)根據直角坐標和極坐標的互化公式x=ρcosθ、y=ρsinθ,把圓C的極坐標方程化為直角坐標方程.(2)由題意可得點A在直線 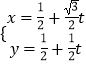 (t為參數)上,把直線的參數方程代入曲線C的方程可得 t2+
(t為參數)上,把直線的參數方程代入曲線C的方程可得 t2+ ![]() t﹣
t﹣ ![]() =0.由韋達定理可得t1t2=﹣
=0.由韋達定理可得t1t2=﹣ ![]() ,根據參數的幾何意義可得|AP||AQ|=|t1t2|的值.
,根據參數的幾何意義可得|AP||AQ|=|t1t2|的值.


科目:高中數學 來源: 題型:
【題目】已知向量 ![]() =(
=( ![]() sinx,﹣1),
sinx,﹣1), ![]() =(cosx,m),m∈R.
=(cosx,m),m∈R.
(1)若m= ![]() ,且
,且 ![]() ∥
∥ ![]() ,求
,求 ![]() 的值;
的值;
(2)已知函數f(x)=2( ![]() +
+ ![]() )
) ![]() ﹣2m2﹣1,若函數f(x)在[0,
﹣2m2﹣1,若函數f(x)在[0, ![]() ]上有零點,求m的取值范圍.
]上有零點,求m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對兩個變量y和x進行回歸分析,得到一組樣本數據:(x1 , y1),(x2 , y2),…,(xn , yn),則下列說法中不正確的是( )
A.由樣本數據得到的回歸方程 ![]() =
= ![]() x+
x+ ![]() 必過樣本中心(
必過樣本中心( ![]() ,
, ![]() )
)
B.殘差平方和越小的模型,擬合的效果越好
C.用相關指數R2來刻畫回歸效果,R2越小,說明模型的擬合效果越好
D.兩個隨機變量的線性相關性越強,相關系數的絕對值越接近于1
查看答案和解析>>
科目:高中數學 來源: 題型:
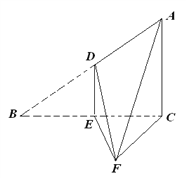
【題目】如圖,直角![]() 中,∠
中,∠![]() ,
,![]() ,D、E分別是AB、BC邊的中點,沿DE將
,D、E分別是AB、BC邊的中點,沿DE將![]() 折起至
折起至![]() ,且∠
,且∠![]() .
.
(Ⅰ)求四棱錐F-ADEC的體積;
(Ⅱ)求證:平面ADF⊥平面ACF.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ex﹣ax﹣1,(a為實數),g(x)=lnx﹣x
(1)討論函數f(x)的單調區間;
(2)求函數g(x)的極值;
(3)求證:lnx<x<ex(x>0)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知F1、F2分別是雙曲線 ![]() 的左右焦點,A為雙曲線的右頂點,線段AF2的垂直平分線交雙曲線與P,且|PF1|=3|PF2|,則該雙曲線的離心率是( )
的左右焦點,A為雙曲線的右頂點,線段AF2的垂直平分線交雙曲線與P,且|PF1|=3|PF2|,則該雙曲線的離心率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于無窮數列![]() ,記
,記![]() ,若數列
,若數列![]() 滿足:“存在
滿足:“存在![]() ,使得只要
,使得只要![]() (
(![]() 且
且![]() ),必有
),必有![]() ”,則稱數列
”,則稱數列![]() 具有性質
具有性質![]() .
.
(Ⅰ)若數列![]() 滿足
滿足![]() 判斷數列
判斷數列![]() 是否具有性質
是否具有性質![]() ?是否具有性質
?是否具有性質![]() ?
?
(Ⅱ)求證:“![]() 是有限集”是“數列
是有限集”是“數列![]() 具有性質
具有性質![]() ”的必要不充分條件;
”的必要不充分條件;
(Ⅲ)已知![]() 是各項為正整數的數列,且
是各項為正整數的數列,且![]() 既具有性質
既具有性質![]() ,又具有性質
,又具有性質![]() ,求證:存在整數
,求證:存在整數![]() ,使得
,使得![]() 是等差數列.
是等差數列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校為了解高三年級學生寒假期間的學習情況,抽取甲、乙兩班,調查這兩個班的學生在寒假期間每天平均學習的時間(單位:小時),統計結果繪成頻率分布直方圖(如圖).已知甲、乙兩班學生人數相同,甲班學生每天平均學習時間在區間[2,4]的有8人.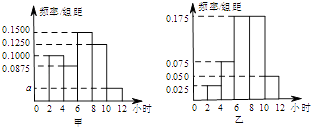
(1)求直方圖中a的值及甲班學生每天平均學習時間在區間(10,12]的人數;
(2)從甲、乙兩個班每天平均學習時間大于10個小時的學生中任取4人參加測試,設4人中甲班學生的人數為ξ,求ξ的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)在R上可導,其導函數為f′(x),且函數y=(1﹣x)f′(x)的圖象如圖所示,則下列結論中一定成立的是( ) 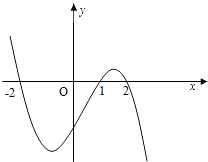
A.函數f(x)有極大值f(2)和極小值f(1)
B.函數f(x)有極大值f(﹣2)和極小值f(1)
C.函數f(x)有極大值f(2)和極小值f(﹣2)
D.函數f(x)有極大值f(﹣2)和極小值f(2)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com